埼玉県立高校入試(2018過去問) 確率と図形問題の解説とポイント

2018年度に行われた埼玉県立高校入試問題第2問、確率と図形問題の小問集合の解説です。
第1問と同じで小問集合ですので難しく考えずに取り組めば確実に拾える問題があります。
ここまでで平均点は十分に超えられるのでじっくり確認しておくと良いですよ。

※（依頼人です。）
第2弾お待たせしました！
第2問の確率と図形編のオリジナル解説と対策です。

こういう系は苦手だからとあきらめちゃってる人っていませんか？
私の息子はあきらめちゃってました。
サッカーはとことん頑張れるのに・・・
友人のお子さんも確率や図形は超苦手でわかるわけないと最初から捨ててるとお母さんは嘆いていました。
でもこれを読んで見て勉強したら「いけるかも！」って、やる気になってくれそうな気がします！
友人が笑顔になってくれる今年信じて・・・

では、超強力な解説と対策をご覧下さい。

問題は埼玉県立総合教育センターにもあります。

⇒　2018埼玉県立高等学校入試問題

第2問小問集合第2弾確率と図形編

サイコロの確率

よく考えたら問題はリンク貼って頂けるんですよね？
書く必要無かったのでは無いかと、今頃気がつきました。

(1)1から6までの目が出る大小1つずつのさいころを同時に1回投げ，大きいさいころの出た目の数を \(a\) ，小さいさいころの出た目を \(b\) とします。\(a\) と \(b\) の積 \(ab\) の約数の個数が3個以上となる確率を求めなさい。
　ただし、大小2つのさいころは，どの目が出ることも同様に確からしいものとします。

さいころは同時に投げても、1個ずつ投げても同じことですよね。

確率は樹形図が基本、だから36通りの樹形図を書けば確実にとれる問題です。
これで樹形図を書いていないとしたら、それは解く気が無いからですよ。
ただ、「約数が3個以上」という条件がついているので、ちょっと長い問題文章とで紛らわしさは感じるかもしれませんね。

文章が長いときは余計な文章は消してしまうとわかりやすいですよ。
例えば、さいころは普通1から6までの出目を持っていますので最初の読点（　、）までは消してかまいません。
最後のさいころの各数字の出る確からしさも消してかまいません。
すると、

　なんてことでしょう！見違えるほど問題がすっきりしました。

最近の中学生はビフォーアフター知らないのか？(T_T)

気を取り直して、

問題は
　『2つのさいころの出目の積が、約数を3個以上持つ確率を求めなさい。』
と変わりました。

約数の説明は必要無いでしょう？
例えば、4の約数は1，2，4の3個あります。
割れる数を探せば数えられるはずですし、3個あった時点で止めても良いのです。

しかし、その必要もありません。

さて、問題を解きますが、確率で樹形図は大事ですが、さいころ2つのときは表が便利です。

	1	2	3	4	5	6
1	1	2	3	4	5	6
2	2	4	6	8	10	12
3	3	6	9	12	15	18
4	4	8	12	16	20	24
5	5	10	15	20	25	30
6	6	12	18	24	30	36

赤数字と青数字がさいころの出目です。
中の黒数字がその積になっています。
この表を書くだけなら1分程度でかけるでしょう？

この中の黒数字で約数を3個以上持つ数字は？
　\(4，6，8，10，12，\cdots\)
と探すより、
　約数が2つ以下の数字を探した方がはやいのでは？
と途中で気がつけば素晴らしいです。

約数が2つ以下の数字は、\(1 , 2 , 3 , 5\)　だけです。

	1	2	3	4	5	6
1	\(\color{magenta}{\fbox{1}}\)	\(\color{magenta}{\fbox{2}}\)	\(\color{magenta}{\fbox{3}}\)	4	\(\color{magenta}{\fbox{5}}\)	6
2	\(\color{magenta}{\fbox{2}}\)	4	6	8	10	12
3	\(\color{magenta}{\fbox{3}}\)	6	9	12	15	18
4	4	8	12	16	20	24
5	\(\color{magenta}{\fbox{5}}\)	10	15	20	25	30
6	6	12	18	24	30	36

積が　\(1 , 2 , 3 , 5\)　となるのは \(7\) 個だけです。

つまり、
　積である数字は全部で 36 個
　約数が3つ以上ある数は \(36-7=29\) 個

求める確率は　\(\displaystyle \color{red}{\frac{29}{36}}\)

約数が3つ以上ある数字を探しても大して時間はかかりませんよ。

確率を出せるかどうかは樹形図か表を書くか、書かないかの違いだけです。

立方体と正八面体の体積比と体積の求め方

(2)1辺の長さが6cmの立方体があります。

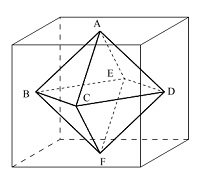
右の図のように，それぞれの面の対角線の
交点をA,B,C,D,E,Fとするとき，
この6つの点を頂点とする正八面体の体積を
求めなさい。

立体をあつかうときは平面を抜き出して考えるとうまくいきます。
空間図形を立体のまま考えられる人は少ないです。
かなりの経験と勘を必要としますので平面を抜き出して考えると良いです。

では、どの面を抜き出すか？
これは有名な問題なので知っている人にとっては簡単なのですが、
立方体の面を抜き出してもなかなか正八面とはつながりません。

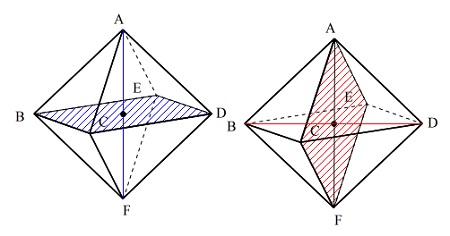
そこで、周りの立方体の面を消して考えると正八面体が見えてきますが、
四角形BCDEと四角形ACFEは正方形でこれを底面とする四角錐2つ分の和、
とみることができればほぼ終わります。

このとき底面とみるのは正方形BCDEか正方形ACFEです。
高さはAFかBDになりますが体積はどちらも同じです。

どちらでも良いのですがここでは底面を正方形ACFEにしましょう。
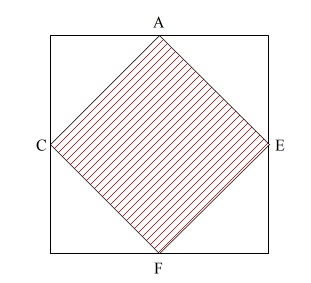
すると底面積は立方体の一面の面積の半分です。

高さはBDですがこの長さは立方体の1辺と同じで6cmです。

底面積の出し方は正方形ACFEの1辺が\(3\sqrt{2}\)だから
　\(3\sqrt{2}\times 3\sqrt{2}=18\,\mathrm{cm^2}\)
と計算しても良いですが、
元の立方体の一面が \(36\,\mathrm{cm^2}\) なので
　\(\displaystyle \frac{1}{2}\times 36=18\,\mathrm{cm^2}\)
とした方がはやいです。

高さは \(6\,\mathrm{cm}\) なのでこの正八面体の体積は、
正方形ACFEを底面とし、高さ \(3\,\mathrm{cm}\) の四角錐2つ分と考えると、

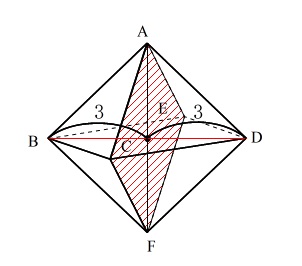
　\(\displaystyle \frac{1}{3}\times 18\times 3\times 2=\underline{36\,\mathrm{cm^3}}\)

となります。

このように対角線などの具体的な長さを求めて体積計算しても良いのですが、
よく考えてみてください。

正八面体の体積は、
　底面積は立方体の　\(\displaystyle \color{red}{\frac{1}{2}}\)
　高さは立方体と同じ
　錐体なので　\(\displaystyle \color{red}{\frac{1}{3}}\)
となっているので、
　元の立方体の \(\displaystyle \frac{1}{6}\)
となっています。
これは直方体に同じ条件で八面体をつくっても同じです。

つまり、元の立方体の体積が
　\(6\times 6\times 6\,\mathrm{cm^3}\)
なので、これを \(\displaystyle \frac{1}{6}\) すれば良いだけです。

正八面体の体積は
　\(\displaystyle \frac{1}{6}\times 6\times 6\times 6=36\,\mathrm{cm^3}\)

辺ACの長さなどを求めるところの説明を省略しましたが、
対角線の長さを求める方法も、基本通りで良いことですよ。
もっと応用された問題ではその方が使い道は多いです。

ここは取りたいところですので少しは時間をかけても良いところです。

ここまでで60点ですが、小問集合ですよね。
1，2問落としたとしても50点は取れます。

ここまでで見直しは決定です。

第2問はまだありますね。

折り目は角の二等分線（垂直二等分線の作図）

(3)下の図のように，△ ABC の辺 AB 上に点 P があります。点 P を通る直線を折り目として，
点 A が辺 BC に重なるように△ ABC を折ります。このとき，折り目となる直線をコンパスと
定規を使って作図しなさい。
　ただし、作図するためにかいた線は，消さないでおきなさい。

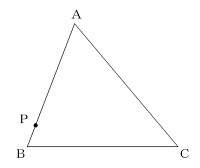
作図問題ですが、コツはコンパスの針の指しどころです。
いくつか練習すればわかってくるので私の説明は必要無いでしょう。

いきなり作図の方法が思いつくわけではないでしょう？

いろいろと試し書きしてみるのが良いです。
別紙に似たような図を書いても良いですし、問題にあたえられた図でも十分試すことはできます。

問題に入りましょう。

頂点 A は、辺 BC 上に折り返され移動します。

折り返しの問題では、どことどこが、元と移動後なのかをできるだけ書き出すと解決します。
このとき、角度も同じところがいくつも出てきますので、すべて書き出すと必ず解決します。

簡単におおよその位置関係を書いてみましょう。

点 P を折り目として、点 A を辺 BC 上に移動させるので、

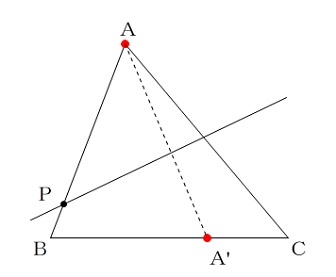
大体ですが、このようになります。
この段階ではおおよその位置関係をつかむだけなので正確で無くてかまいません。

「折り返した」ということは等しいところがあるはずです。
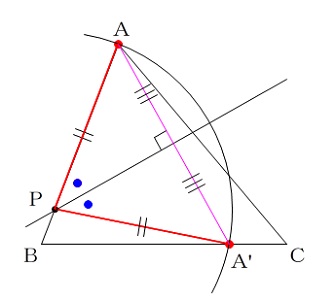
例えば、わかりやすいのは辺 PA と辺 PA’ ですね。

辺の長さを等しく作図するのはコンパスです。
点 P に針を刺し、円を描いて辺 BC と交わった点が A’ です。

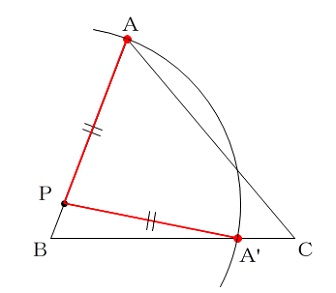
ここまで来れば折り目の作図は簡単で、
　\(\angle APA’　の二等分線\)
が折り目になります。

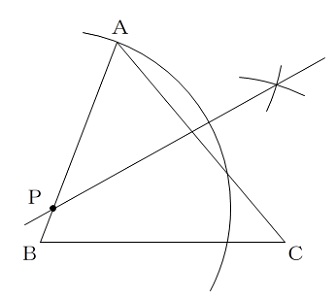
（答えの作図）

ちなみに点 P は、辺 AA’ の垂直二等分線上にありますが作図に書き込む必要はありません。

指示されたものをできるだけ簡単に、見てわかるように書き残す、それが作図問題の答えになります。

点 A’ を書き込んだ後、辺 AA’ を結んで、辺 AA’ の垂直二等分線を作図しても必ず点 P を通るので、
その方針を作図として示しても正解にはしてくれるでしょう。

円周角の定理と相似の証明

(4)右の図のように，円周上に4 点 A,B,

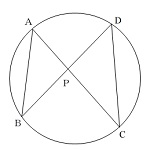
C,D をとり，線分 AC とBD との交点
を P とします。
　このとき，PA : PD = PB : PC である
ことを証明しなさい。

「辺の比が等しいことを証明しなさい」となっていますが、
辺の比が等しいことを証明するのは相似の利用になります。
つまり、相似の証明と同じことです。

辺の長さが等しいことは、合同の証明をすることで示す場合がほとんどで、
たまに三平方の定理などを使って実際の長さ、距離を求めて示します。

これは円周角の定理を覚えていれば簡単に終わりますので早速問題に入りましょう。

　【円周角の定理】
同一の弧、または同一長の弧に対する円周角はいつも等しい。

これは教科書にもあるので説明を省きます。
（ちょっと長くなりすぎている気がしますので。）

円周角が等しくなる角に印を書き込みます。
図形の証明問題は図の中で完結させる、というのは当たり前のことなので説明は必要無いでしょう。

対頂角が等しいことを使っても良いですし、
円周角1つで証明は簡単に終わります。

必ず書いておくべき部分を赤字にしておきます。

証明）
　\(\color{red}{\triangle \mathrm{PAB}　と　\triangle \mathrm{PDC}　において}\)　
円周角の定理より、
　\(\angle \mathrm{PAB}=\angle \mathrm{PDC}　･･･①\)
　\(\angle \mathrm{PBA}=\angle \mathrm{PCD}　･･･②\)　
①②より、
　2組の角がそれぞれ等しいので、
　\(\color{red}{\triangle \mathrm{PAB}　∽　\triangle \mathrm{PDC}}\)　
よって、
　\(\mathrm{\color{red}{PA : PD = PB : PC}}\)
（証明終わり）

証明部分は対頂角を使っても良いですが、相似条件は必ず書きましょう。

証明）
　\(\triangle \mathrm{PAB}　と　\triangle \mathrm{PDC}　において\)　　
　\(\angle \mathrm{PAB}=\angle \mathrm{PDC}　（円周角の定理）\)　
　\(\angle \mathrm{APB}=\angle \mathrm{DPC}　（対頂角）\)
　2組の角がそれぞれ等しいので、
　\(\triangle \mathrm{PAB}　∽　\triangle \mathrm{PDC}\)　
よって、
　\(\mathrm{PA : PD = PB : PC}\)
（証明終わり）

証明を書くときに論理の組み立てが苦手な人は、
この証明のように条件の理由を後ろに（かっこ）をつけて付け足せば良いです。
数学で後書きするのは、∵）（because の意味）を加えますが中学生は無くても良いです。

部分点があるらしいので、配点を分けてみると、
　相似の条件２つ（２点）
　相似条件と相似（２点）
　結論（これが無いと証明ではありません。）
これらは書いておかないと減点対象になります。
全体が論理的に通じて７点満点となるのではないでしょうか。