2019年(平成31年)度に埼玉県で行われた公立高校入試数学の問題と解説です。
全部で大問が4つあり、小問も割とありますので長くなから各問ごとに分けて説明しておきます。
一部学校選択問題と同じ問題がありますが、気にする程難しいものではありません。
※（依頼人です。）
2019年(平成31年)度埼玉県公立高校入試終わりましたね。
受験生のみなさん、お父さんお母さんお疲れさまでした。
早速、受験個別指導のプロとして全国で活躍されているこの時期劇的にお忙しい柏田先生に無理を言ってお願いし2019年(平成31年)度の埼玉県公立高校入試の数学の解説をしていただきました。
今回の解説も前回（2018年 平成30年度）同様、永久保存版にしても良いくらい価値がありますよ。
では、超強力な解説をご覧下さい。
問題は埼玉県の公式ページでも公開してくれています。
式の計算、方程式、関数、図形の基本小問集合
\(\large{1}\)
小問集合が並んでいますが、ミスさえ気をつければ考えるような問題はありません。
式の計算と文字式の計算
(1)
\(\hspace{10pt}-2a+5a\\
=\underline{ 3a }\)
同類項をまとめただけです。
(2)
\(\hspace{10pt}(-8)\div (-4)-1\\
=2-1\\
=\underline{ 1 }\)
足し算引き算より、かけ算割り算が先ですね。
割り算を逆数のかけ算にするという基本が身についている人は、
\(\hspace{10pt}(-8)\color{blue}{\div (-4)}-1\\
\displaystyle =(-8)\color{blue}{\times \frac{1}{(-4)}}-1\\
\displaystyle =\frac{8}{4}-1\\
=2-1\\
=\underline{ 1 }\)
として良いですが符号にだけは気をつけておきましょう。
この後も注意点は昨年度の解説でていねいにしているのでここでは最小限にしておきます。
⇒ 埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策
(3)ややこしくなりそうですが割り算の直後は分母へ、という計算にすれば単なる約分問題です。
\(\hspace{10pt}3x^2\color{red}{\div(-y^3)}\times 2xy^3\\
\displaystyle =\frac{3x^2\times 2xy^3}{\color{red}{-y^3}}\\
=\underline{ -6x^3y }\)
割り算は逆数のかけ算なので
\(\hspace{10pt}3x^2\color{blue}{\div(-y^3)}\times 2xy^3\\
\displaystyle =3x^2\color{blue}{\times \frac{1}{-y^3}}\times 2xy^3\\
=\underline{ -6x^3y }\)
でも良いですが分母と分子をはっきり分けて計算した方が約分間違いは減ります。
符号は奇数回かかっているので全体はマイナスです。
符号を忘れないように気をつけておきましょう。
無理数の計算と因数分解
(4)無理数の分母の有理化と引き算です。
\(\hspace{10pt}\displaystyle \frac{10}{\sqrt{5}}-\color{blue}{\sqrt{45}}\\
\displaystyle =\frac{10\color{red}{\times \sqrt{5}}}{\sqrt{5}\color{red}{\times \sqrt{5}}}-\color{blue}{3\sqrt{5}}\\
\displaystyle =\frac{10\sqrt{5}}{5}-3\sqrt{5}\\
\displaystyle =2\sqrt{5}-3\sqrt{5}\\
=\underline{ -\sqrt{5} }\)
素因数分解は問題用紙の片隅にでも書いて確実にやっておいた方が良いですよ。
\(\color{magenta}{3}\,\underline{)\,45}\\
\color{magenta}{3}\,\underline{)\,15}\\
\hspace{16pt}5\)
1つの計算ミスで\(\,4\,\)点です。
(5)因数分解です。
\(x^2+6x-27\)
定数項\(\,-27\,\)に着目します。
かけて\(\,27\,\)になるのは
\(\color{black}{\fbox{ 1 × 27 }}\) \(\color{red}{\fbox{ 3 × 9 }}\)
だけです。
かけて定数項の\(\,\color{red}{-27}\,\)
足して\(\,x\,\)の\(\,1\,\)次の項の係数\(\,\color{blue}{6}\,\)になるのは
\(\color{red}{(-3)\times 9=-27}\)
\(\color{blue}{(-3)+9=6}\)
なので
\(\hspace{10pt}x^2+6x-27\\
=\underline{ (x-3)(x+9) }\)
連立方程式と2次方程式
(6)連立方程式を解くだけですが、代入法でも加減法でもどちらでもかまいません。
代入法の方が楽な問題です。
\( \begin{cases}
\hspace{7pt} \color{red}{y}=\color{blue}{5-3x} ･･･①\\ \\
\hspace{7pt} x-2\color{red}{y}=4 ･･･②
\end{cases}\)
①の\(\,y\,\)を②の\(\,y\,\)に代入します。
\(\begin{eqnarray}
x-2(\color{red}{\color{blue}{5-3x}})&=&4\\
x-10+6x&=&4\\
x+6x&=&4+10\\
7x&=&14\\
x&=&2
\end{eqnarray}\)
この\(\,x=2\,\)を①か②に戻せば良いのですが、もちろん①に戻しましょう。
\(\begin{eqnarray}
y&=&5-3\times (2)\\
&=&5-6\\
&=&-1
\end{eqnarray}\)
答え \(\,\underline{ x=2\,,\,y=-1 }\,\)
加減法を使って解くと
\( \begin{cases}
\hspace{7pt} y=5\color{red}{-3x} ･･･①\\ \\
\hspace{7pt} x-2y=4 ･･･②
\end{cases}\)
①の\(\,\color{red}{-3x}\,\)を移項して
\(3x+y=5 ･･･①’\)
これと②を連立して
\( \begin{cases}
\hspace{7pt} 3x+y=5 ･･･①’\\ \\
\hspace{7pt} x-2y=4 ･･･②
\end{cases}\)
連立方程式を解くときの方針は一文字消去です。
どちらの文字を消去しても良いですが、ここでは\(\,y\,\)を消去しましょう。
\(\,①’\,\)を両辺\(\,2\,\)倍して両辺を足します。
\(\hspace{14pt}6x+2y=10\\
\underline{+)\hspace{7pt}x-2y=\hspace{4pt}4}\\
\hspace{14pt}7x\hspace{20pt}=14\\
\hspace{39pt}x=\hspace{4pt}2\)
これを\(\,①②①’\,\)のどれでも良いのですが①に戻すと\(\,y\,\)の値が直接出ます。
(7)『2次方程式を解く』ことと、『2次方程式の解を求める』ことは同じことです。
2次方程式を解くときは因数分解から試すのが良いですが\(\,x^2\,\)の係数が\(\,1\,\)ではなく、共通因数もないので解の公式です。
今さら必要無いとは思いますが、\(\,2\,\)次方程式の解の公式です。
2次方程式
\(ax^2+bx+c=0\)
の解は
\(\displaystyle \color{red}{x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}\)
\(\,2\,\)次方程式は
\(2x^2-3x-1=0\)
よって解は
\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-3)\pm\sqrt{(-3)^2-4\times (2)\times (-1)}}{2\times 2}\\
&=&\frac{3\pm\sqrt{9+8}}{4}\\
&=&\underline{ \frac{3\pm\sqrt{17}}{4} }
\end{eqnarray}\)
代入するときは計算ミスを減らすため（かっこ）をつけて代入するのが基本です。
1次関数の求め方
(8)\(\,2\,\)点を通る直線の方程式、\(\,1\,\)次関数を求める問題です。
\(\,(\hspace{8pt}4\,,\,3)\,\)
\(\,(-2\,,\,0)\,\)
\(\,1\,\)次関数の傾きと変化の割合は一致するので
\(\displaystyle \color{red}{(変化の割合)=\frac{ (\,y\,の増加量\,) }{ (\,x\,の増加量\,) }}\)
を利用しますが、変化量を求めるときに\(\,x,y\,\)ともに同じ方向に引きます。
引く方向が違うと変化の割合の符号が逆になります。
ここではどちらも下から上を引いておきます。
\(\,(\,x\,の増加量\,)=(-2)-(4)=-6\,\)
\(\,(\,y\,の増加量\,)=0-(3)=-3\,\)
これから
\(\displaystyle (傾き)=\frac{-3}{-6}=\frac{1}{2}\)
求める\(\,1\,\)次関数は
\(\displaystyle y=\frac{1}{2}x+b\)
とおけて、与えられた\(\,2\,\)点のどちらも通るのでどちらかを代入して\(\,b\,\)（\(\,y\,\)切片）を求めます。
\(\,(-2\,,\,0)\,\)を代入すると
\(\begin{eqnarray}\displaystyle
0&=&\frac{1}{2}\times (-2)+b\\
-b&=&-1\\
b&=&1
\end{eqnarray}\)
よって求める\(\,1\,\)次関数は
\(\displaystyle \underline{ y=\frac{1}{2}x+1 }\)
もちろんもう一つの点\(\,(\,\color{red}{4}\,,\,\color{blue}{3})\,\)も通ります。
\(\displaystyle y=\frac{1}{2}\times (\color{red}{4})+1=\color{blue}{3}\,\)
これが合わなければ計算ミスしていますので検算に使うと良いです。
角度を求める方法
(9) \(\color{red}{\fbox{ 学校選択問題の1の(5) }}\)
三角定規が重なっている図形の角度を求めます。
角度を求める問題は分かるところを次々に書き込んで行けば自ずと答えが出ます。
答えが出せないのは図に書き込まないからで、『分からない』のではなく『解く気がない』です。
どこからでも良いので分かる角度を書き込んで見て下さい。
三角定規のそれぞれの角度です。
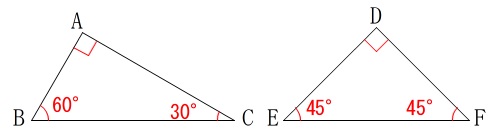
このことから図\(\,2\,\)のそれぞれの角度は、
（途中まで入れてあります。）
それぞれの角度の求め方は、
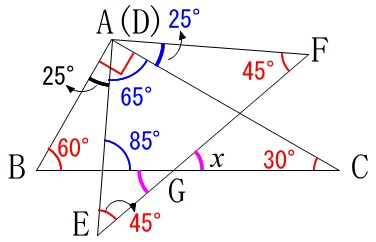
最初に出てくるのは
\(\begin{eqnarray}
\mathrm{∠EAC}&=&\mathrm{∠BAC-∠BAE}\\
&=&90^{\circ}-25^{\circ}\\
&=&\color{blue}{65^{\circ}}
\end{eqnarray}\)
から
\(\begin{eqnarray}
\mathrm{∠FAC}&=&\mathrm{∠EAF-∠EAC}\\
&=&90^{\circ}-65^{\circ}\\
&=&\color{blue}{25^{\circ}}
\end{eqnarray}\)
だと思うのですが、\(\,\color{blue}{85°}\,\)の方に進んだ人もいるかもしれません。
他にもいろいろな角度が分かります。
（すべての角度は出てきます。）
しかし、
三角形の内角の和は常に\(\,180°\,\)で一定
だということを利用すれば、
対頂角は等しいので残りの二角の和が等しくなることから
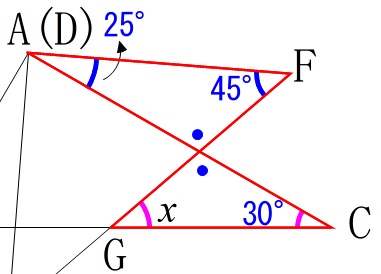
\(\mathrm{∠FAC+∠AFC=∠ACG+∠FGC}\)
なので
\(\begin{eqnarray}
25^{\circ}+45^{\circ}&=&30^{\circ}+x\\
70^{\circ}&=&30^{\circ}+x\\
x&=&40^{\circ}
\end{eqnarray}\)
と求めるのが一番はやいでしょう。
それほど変わりませんのでどっちでも良いです。
\(\,\color{blue}{85°}\,\)に降りたとすれば
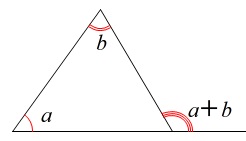を利用すると楽ですね。
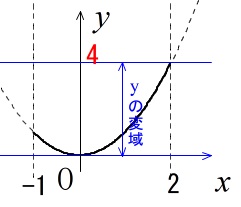
原点を通る放物線（２次関数）の性質
(10) \(\color{red}{\fbox{ 学校選択問題の1の(6) }}\)
関数の問題です。
関数は\(\,y=x^2\,\)
甘く見てグラフを書かずに考えるなんてことはやめておきましょう。
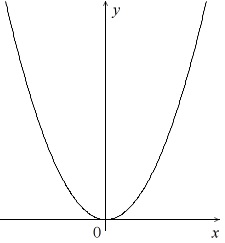下に凸な放物線です。（上に開いた放物線です。）
ア
関数\(\,y=x^2\,\)で
\(\,x=3\,\)のとき\(\,y=3^2=9\,\)
なので正しくありません。
イ
放物線はすべて軸に対称です。
この放物線は頂点が原点なので\(\,y\,\)軸が対称の軸で正しい。
ウ
定義域（\(\,x\,\)の変域）が\(\,-1\,≦\,x\,≦\,2\,\)のときの値域（\(\,y\,\)の変域）は
\(\,x=-1\,\)のときの値は関係ありません。
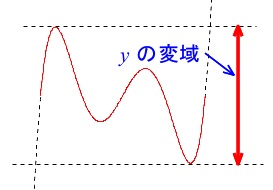
最小値は\(\,x=0\,\)のときの\(\,y=0\,\)なので
\(\,y\,\)の変域は\(\,0\,≦\,y\,≦\,4\,\)
正しくない。
エ
変化の割合は
\(\displaystyle (変化の割合)=\frac{ \color{blue}{(\,y\,の増加量\,)} }{ \color{red}{(\,x\,の増加量\,)} }\)
です。（8)にもあります。
\(\,x\,\)が\(\,2\,\)から\(\,4\,\)まで増加するときの\(\,y\,\)の変化量を求めます。
関数\(\,y=x^2\,\)の\(\,x=2,4\,\)のそれぞれの座標を出して増加量を見れば良いです。
\((\,2\,,\,4\,)\)
\((\,4\,,\,16\,)\)
なので
\(\color{red}{(\,x\,の増加量\,)}=4-2=\color{red}{2}\)
\(\color{blue}{(\,y\,の増加量\,)}=16-4=\color{blue}{12}\)
よって
\(\begin{eqnarray}\displaystyle
(変化の割合)&=&\frac{ \color{blue}{(\,y\,の増加量\,)} }{ \color{red}{(\,x\,の増加量\,)} }\\
&=&\frac{\color{blue}{12}}{\color{red}{2}}\\
&=&6
\end{eqnarray}\)
正しい。
オ
関数の増減です。
関数\(\,y=x^2\,\)のグラフを見れば明らかです。
\(\,x\,\)が増加するということはグラフで左から右に移動するということです。
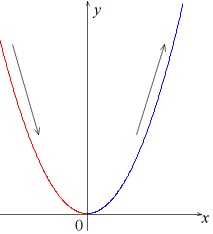
\(\,\color{red}{x\,＜\,0}\,\)の範囲では\(\,x\,\)が増加すれば\(\,y\,\)は減少
\(\,\color{blue}{x\,＞\,0}\,\)の範囲では\(\,x\,\)が増加すれば\(\,y\,\)は増加
しています。
正しくない。
答え \(\,\underline{ イ と エ }\,\)
規則と整数の性質
(11) \(\color{red}{\fbox{ 学校選択問題の1の(8) }}\)
この問題は規則性の問題と連立方程式と見せかけた整数問題です。
布の枚数は整数なので数えていけば①の答えは出てくるでしょう。
問題の条件を整理しておきましょう。
長さ\(\,\mathrm{50\,cm}\,\)と長さ\(\,\mathrm{30\,cm}\,\)を重ねて\(\,\mathrm{5\,m}\,\)にする。
幅は\(\,\mathrm{5\,cm}\,\)重ねる。
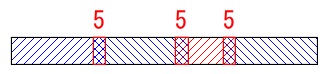隣り合う布が\(\,\mathrm{5\,cm}\,\)重なるようにつなげるということです。
縦の長さは関係ありません。
いろいろな考え方ができますので解法もいろいろと出てくるでしょう。
いくつか紹介しておきますが解答例に過ぎませんので、自分の解法で合っているかは学校の先生にでも聞いて下さい。
①
\(\,\mathrm{50\,cm}\,\)の長さの布だけを使って\(\,\mathrm{5\,m}\,\)にします。
\(\,\mathrm{5\,m}\,\)は\(\,\mathrm{500\,cm}\,\)です。
単位をそろえたので後は単位抜きで書き出します。
重ねる幅は\(\,5\,\)なので
\(\,1\,\)枚で\(\,50\,\)
\(\,2\,\)枚で\(\,50+45\,\)
\(\,3\,\)枚で\(\,50+45+45\,\)
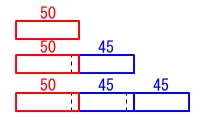
と見ると、
\(\,50+45\times 10=500\,\)
となるので加える枚数が\(\,10\,\)枚なので\(\,\underline{ 11 }\,\)枚
これを一般的に表すと\(\,n\,\)枚の布を継ぐとすると、足される\(\,45\,\)は\(\,(\,n-1\,)\,\)枚なので
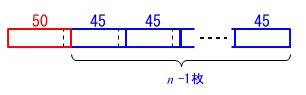
\(\,50+(n-1)45=500\,\)
を解けば出てきます。
または、
\(\,50\,\)の長さが\(\,n\,\)枚重ねられていないときの長さは\(\,50n\,\)
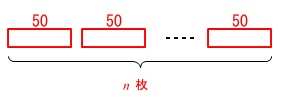
重なり\(\,5\,\)は\(\,(\,n-1\,)\,\)回あるので全体の長さは\(\,5(n-1)\,\)減るので
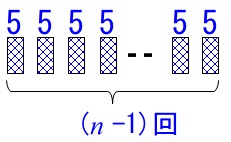全体の長さは
\(\hspace{10pt}50n-5(n-1)\\
=50n-5n+5\\
=45n+5\)
と表せるので
\(\begin{eqnarray}
45n+5&=&500\\
45n&=&500-5\\
&=&495\\
n&=&\underline{ 11 }
\end{eqnarray}\)
②
今度は\(\,50\,\)と\(\,30\,\)を両方使って\(\,500\,\)にします。
重なりは同じ\(\,5\,\)なので、重なりのない長さから重なりを引く方向で解答します。
\(\,50\,\)を\(\,x\,\)枚、\(\,30\,\)を\(\,y\,\)枚使って\(\,500\,\)にするとすると,
重なりを考えない場合の長さは
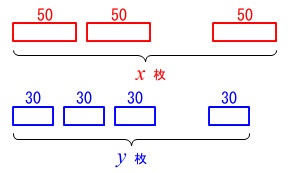
\(\color{red}{50x}+\color{blue}{30y}\)
全体の枚数は\(\,x+y\,\)なので重なりは\(\,x+y-1\,\)回あります。
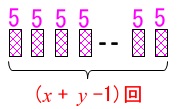
\(\,1\,\)回の重なりは\(\,5\,\)だから\(\,(x+y-1)\,\)回の重なりで減る長さは
\(\,\color{magenta}{5(x+y-1)}\,\)
重なり部分を引いた全体の長さは
\(\hspace{10pt}50x+30y-5(x+y-1)\\
=50x+30y-5x-5y+5\\
=45x+25y+5\)
これが\(\,500\,\)になるので
\(\begin{eqnarray}
45x+25y+5&=&500\\
45x+25y&=&495\\
9x+5y&=&99
\end{eqnarray}\)
これを満たす整数\(\,x,y\,\)を探すと、
\(\,x=1\,\)のとき\(\,y=18\,\)
\(\,x=6\,\)のとき\(\,y=9\,\)
よって
\(\,\underline{ 赤い布\,1\,枚と白い布\,18\,枚 }\,\)
と
\(\,\underline{ 赤い布\,6\,枚と白い布\,9\,枚 }\,\)
の組だけです。
\(\,x=11,y=0\,\)も方程式は満たしますが、
『両方使う』ので\(\,y=0\,\)は条件を満たしません。
文字が2つあるので連立方程式だと感じますが、他に条件はありません。
あるのは枚数という『整数』であることだけです。
整数という場合は調べ尽くすことがポイントになります。
\(\begin{eqnarray}
9x+5y&=&99\\
5y&=&99-9x\\
y&=&\frac{9(11-x)}{5}
\end{eqnarray}\)
と変形できれば\(\,y\,\)も整数なので、
\(\,11-x\,\)が\(\,5\,\)の倍数
と絞ることはできますが、すべて調べてもしれています。
整数をあつかうときは、文字の数より条件が少ないことがあるので気をつけておきたいですね。
⇒ 2019年(平成31年)度埼玉県公立高校入試数学第2問の解説
\(\large{2\})は標本調査と体積問題、作図と証明です。
本当はここまでを前半としたかったのですがちょっと長くなりました。
それと、\(\large{1}\,\)だけで配点は\(51\)点あります。
前半とするにはちょうど良いのではないでしょうか。笑
（めんどくさくなったからではありませんよ。）
⇒ 2019年(平成31年)度埼玉県公立高校入試数学第2問の解説
2019年(平成31年)度埼玉県公立高校入試 数学第2問のオリジナル解説です。
⇒ 2019年度埼玉県公立高校入試数学第3問4問(同学校選択問題)の解説
2019年度埼玉県公立高校入試 数学第3問・4問(同学校選択問題)のオリジナル解説になります。
⇒ 埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策
\(2018\)年の問題でも詳しく解説していますので見ておくと良いです。