2019年(平成31年)度に埼玉県で行われた公立高校入試数学の第2問の解説です。
第2問は標本調査と三角すいの部分体積を求める問題、それに作図と平行四辺形の証明です。
標本調査の問題と作図は学校選択問題と同じですが注意点が1つだけあります。
※（依頼人です。）
2019年(平成31年)度埼玉県公立高校入試終わりましたね。
受験生のみなさん、お父さんお母さんお疲れさまでした。
早速、受験個別指導のプロとして全国で活躍されているこの時期劇的にお忙しい柏田先生に無理を言ってお願いし2019年(平成31年)度の埼玉県公立高校入試の数学の解説をしていただきました。
今回の解説も前回（2018年 平成30年度）同様、永久保存版にしても良いくらい価値がありますよ。
では、2問目の超強力な解説をご覧下さい。
問題は埼玉県の公式ページでも公開してくれています。
２．標本調査、体積、作図、証明問題
\(\large{2}\)
標本調査は比例式による推測
(1) \(\color{red}{\fbox{ 学校選択問題の1の(7) }}\)
標本調査の問題は比例式ですぐに終わりますが、この問題では1つだけ注意点があります。
白いペットボトルのキャップとオレンジ色のキャップとありますが、
白と黒の碁石でも同じです。
袋に入った白があって\(\,50\,\)個オレンジを加えた。
\(\,\color{blue}{30}\,\)個取り出したら\(\,\color{blue}{6}\,\)個オレンジだった。
（これが全体とオレンジの比率です。）
一部を取り出す標本調査になりますので、推測の答えになります。
ただ、ここではオレンジを\(\,\color{blue}{50}\,\)個加えたので、
元の袋に入っていた白を\(\,\color{red}{x}\,\)個とすると全体は\(\,\color{red}{x}+\color{blue}{50}\,\)
となっていることに注意が必要です。
\(\begin{eqnarray}
30：6&=&(x+50):50\\
6(x+50)&=&50\times 30\\
x+50&=&\frac{50\times 30}{6}\\
x+50&=&250\\
x&=&200
\end{eqnarray}\)
よって およそ \(\,\underline{ 200 } \,\)個
これを
\(\begin{eqnarray}
30：6&=&x:50\\
6x&=&50\times 30\\
x&=&\frac{50\times 30}{6}\\
&=&250
\end{eqnarray}\)
とした場合は、加えたオレンジ\(\,50\,\)個を引かなくてはなりません。
三角錐の体積の求め方
(2)
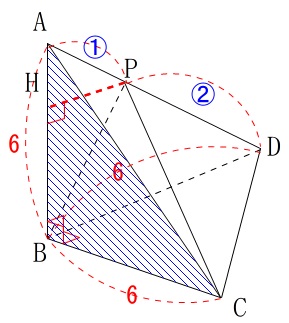
『右の図のような』とあるのですが条件がすべて書き込まれているわけではありません。
足りない部分は自分で書き込んで、図の中でできるだけ分かり易くししておくというのが図形問題の基本です。
\(\color{red}{\fbox{条件}}\)
\(\,\mathrm{AB=BC=BD=6}\,\)
\(\,\mathrm{∠ABC=∠ABD=∠CBD=90^{\circ}}\,\)
\(\,\mathrm{AP:PD=1:2}\,\)
求めるのは三角錐\(\,\mathrm{PBCD}\,\)の体積です。
三角錐の体積を求めるには底面も高さも分かっていません。
なので公式は直接使えそうもありません。
公式が使えない場合の面積や体積を求めるときは、
『部分』＋『部分』
『全体』－『部分』
を考えるとうまくいくことが多いです。
先ずは全体（三角錐\(\,\mathrm{ABCD}\,\)）体積を出しておきましょう。
底面は\(\,\mathrm{△ABC}\,\)でも\(\,\mathrm{△BCD}\,\)でもどちらも直角三角形で、
高さになる垂線の長さも分かりますのでどちらでも良いです。
図で下にあるので底面を\(\,\mathrm{△BCD}\,\)としましょう。
このとき高さは\(\,\mathrm{AB}\,\)です。
底面積を出します。
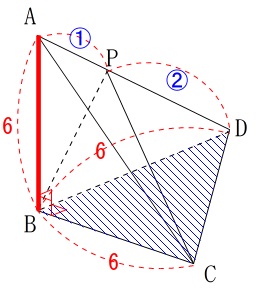
立体問題を簡単にする一番の方法は面を抜き出すことです。
\(\,\mathrm{△BCD}\,\)は直角二等辺三角形です。
底面積は
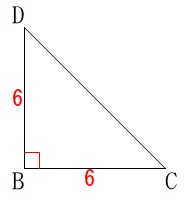
\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{BD}\\
&=&\frac{1}{2}\times 6\times 6\\
&=&18
\end{eqnarray}\)
高さは\(\,\mathrm{AB=6}\,\)なので三角錐\(\,\mathrm{ABCD}\,\)の体積は
\(\begin{eqnarray}
\mathrm{ABCD}&=&\frac{1}{3}\times \mathrm{△BCD}\times \mathrm{AB}\\
&=&\frac{1}{3}\times 18\times 6\\
&=&\color{red}{36}
\end{eqnarray}\)
ここからは大きく3つの方法に分かれます。
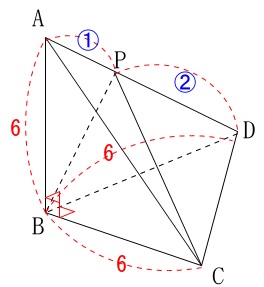
三角錐\(\,\mathrm{ABCD}\,\)から三角錐\(\,\mathrm{ABCP}\,\)を引く。
三角錐\(\,\mathrm{PBCD}\,\)の体積を直接求めに行く。
もう一つは、三角錐\(\,\mathrm{ABCD}\,\)を圧縮する。
全部やっておきます。
三角錐\(\,\mathrm{ABCD}\,\)から三角錐\(\,\mathrm{ABCP}\,\)を引く。
この場合は底面が\(\,\mathrm{△ABC}\,\)で高さが図の\(\,\mathrm{PH}\,\)になります。
\(\,\mathrm{PH}\,\)が必要なので\(\,\mathrm{△ABD}\,\)を抜き出します。
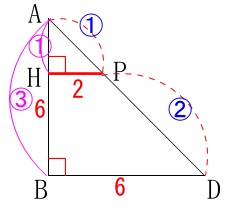\(\,\mathrm{△AHP}\,\) ∽ \(\,\mathrm{△ABD}\,\)
で
\(\,\mathrm{AP:PD=1:2}\,\)なので相似比は\(\,\mathrm{AH:AB}\,\)の\(\,1：3\,\)
このことから
\(\begin{eqnarray}
1:3&=&\mathrm{PH:DB}\\
3\mathrm{PH}&=&\mathrm{DB}\\
3\mathrm{PH}&=&6\\
\mathrm{PH}&=&2
\end{eqnarray}\)
よって三角錐\(\,\mathrm{PABC}\,\)の体積は
\(\begin{eqnarray}\displaystyle
\mathrm{PABC}&=&\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{PH}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 6\times 2\\
&=&\color{blue}{12}
\end{eqnarray}\)
求める三角錐\(\,\mathrm{PBCD}\,\)の体積は
\(\begin{eqnarray}\displaystyle
\mathrm{PBCD}&=&\mathrm{ABCD}-\mathrm{PABC}\\
&=&\color{red}{36}-\color{blue}{12}\\
&=&\underline{ 24 }
\end{eqnarray}\)
三角錐\(\,\mathrm{PBCD}\,\)の体積を直接求めに行く。
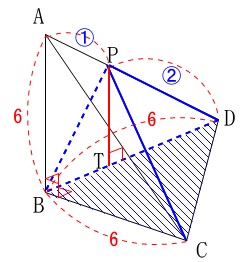この場合は底面を\(\,\mathrm{△BCD}\,\)、高さを図の\(\,\mathrm{PT}\,\)とします。
高さとなる\(\,\mathrm{PT}\,\)の長さが欲しいので\(\,\mathrm{△ABD}\,\)をぬきだします。
\(\,\mathrm{△DTP}\,\) ∽ \(\,\mathrm{△DBA}\,\)
で\(\,\mathrm{AP:PD=1：2}\,\)なので相似比となる\(\,\mathrm{DT:DB=PT:AB=2:3}\,\)
なので
\(\begin{eqnarray}\displaystyle
2:3&=&\mathrm{PT:AB}\\
3\mathrm{PT}&=&2\mathrm{AB}\\
&=&2\times 6\\
\mathrm{PT}&=&4
\end{eqnarray}\)
よって三角錐\(\,\mathrm{PBCD}\,\)の体積は
\(\begin{eqnarray}\displaystyle
\mathrm{PBCD}&=&\frac{1}{3}\times \mathrm{\color{blue}{△BCD}}\times \mathrm{\color{red}{PT}}\\
&=&\frac{1}{3}\times \color{blue}{\frac{1}{2}\times 6\times 6}\times \color{red}{4}\\
&=&\underline{ 24 }
\end{eqnarray}\)
もう一つの三角錐\(\,\mathrm{ABCD}\,\)を圧縮する、というのは上の2つを簡単にしたものです。
やっていることは同じなので会員向けに簡単に解答しておきます。
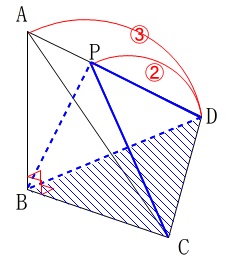
\(\,\mathrm{ABCD}\,\)の体積は\(\,36\,\)で頂点を\(\,\mathrm{D}\,\)とみたとき、
\(\displaystyle \mathrm{DP=\frac{2}{3}\times DA}\,\)
\(\displaystyle \mathrm{DC}=\frac{1}{1}\times \mathrm{DC}\)
\(\displaystyle \mathrm{DB}=\frac{1}{1}\times \mathrm{DB}\)
なので求める三角錐の体積は
\(\begin{eqnarray}
\mathrm{PBCD}&=&36\times \frac{2}{3}\times \frac{1}{1}\times \frac{1}{1}\\
&=&\underline{ 24 }
\end{eqnarray}\)
この問題はこの手法は使うまでもないですね。
上の2つとやっていることは同じです。
作図の考え方
(3) \(\color{red}{\fbox{ 学校選択問題の2の(1) }}\)
\(\,105°\,\)の作図です。
作図で使うのは基本的に2つ、
垂線を引く。
角の二等分線を描く。
です。
ただ、ここでは\(\,60°\,\)の作図を必要とするので正三角形を利用します。
\(\,105°\,\)の作図は直接できないので\(\,105°\,\)を分解するか、
垂線の\(90°\)に\(30°\)の二等分線を加えるか、
\(105°\)の\(\,2\,\)倍の\(\,210°\,\)を作図して、その角の二等分線を引くかです。
ここでは分解を利用しますが、2つの順番があります。
\(\,105°=\color{red}{45°}+\color{blue}{60°}\,\)
の順番で作図するか
\(\,105°=\color{blue}{60°}＋\color{red}{45°}\,\)
の順番で作図するかです。
つまり垂線の二等分線が先か、正三角形が先かということですが同じことですのでどちらでも良いです。
\(\,105°=\color{red}{45°}+\color{blue}{60°}\,\)
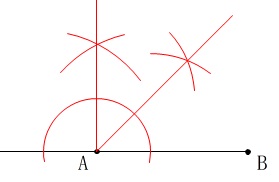\(\,45°\,\)の作図です。
\(\,\mathrm{AB}\,\)を延長して、\(\,\mathrm{A}\,\)を通る垂線を引き、その\(\,90°\,\)の角の二等分線を描きました。
後は\(\,45°\,\)の線の一部を\(\,1\,\)辺とする正三角形を描けば\(\,60°\,\)が加わります。
\(\,1\,\)辺は適当に決めて良いですが、半径が等しいことを利用するとはやいですね。
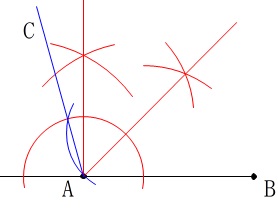正三角形は半径\(\,2\,\)つと弦でできています。
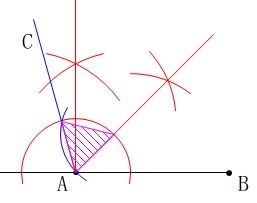
\(\,105°=\color{blue}{60°}＋\color{red}{45°}\,\)
\(\,60°\,\)を作るために正三角形を先に描くと、
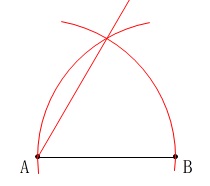\(\,1\,\)辺が\(\,\mathrm{AB}\,\)の正三角形を描くことで\(\,60°\,\)を作図しました。
次にこれを延長して\(\,\mathrm{A}\,\)から垂線を描き、角の二等分線を書き足します。
\(\,\mathrm{A}\,\)から垂線を引いたときの弧を利用して角の二等分線を描きました。
平行四辺形になる条件は候補５つ
(4)
平行四辺形であることの証明です。
平行四辺形の成立条件は5つあります。
教科書にあるので確認しておいてください。
この5つの条件をすぐにいえるかどうかは、
数学の言葉の重要性を理解しているかどうかを測るのに適しています。
すぐに言えれば良いですが、言えない人は数学が苦手に感じているのではないでしょうか。
数学の大切なポイントが分かっていないからですよ。
高校の数学も含んでますけど、中学数学のすべてはここにあります。（宣伝です。笑）
この過去問もすべて『覚え太郎』の中から解説しています。
さて、宣伝も終わったところで証明しましょう。
証明は簡単です。
図形の証明は図の中で完成させておくことがポイントです。
図の中で示せていないのに、日本語の文章にできるわけがないでしょう。
\(\color{red}{\fbox{条件}}\)
\(\,\mathrm{ABCD}\,\)は平行四辺形
対角線の交点は\(\,\mathrm{O}\,\)
\(\,\mathrm{E,F}\,\)は線分\(\,\mathrm{OA,OC}\,\)上の点で\(\,\mathrm{AE=CF}\,\)
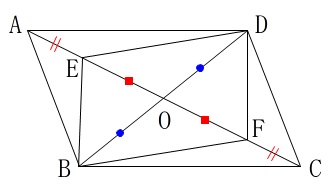証明は終わってますね。
（証明）
\(\,\mathrm{ABCD}\,\)は平行四辺形で対角線はそれぞれの中点で交わるので
\(\mathrm{\color{red}{AO}=\color{red}{CO}} ･･･①\)
\(\mathrm{\color{blue}{BO}=\color{blue}{DO}} ･･･②\)
また
\(\mathrm{EO=\color{red}{AO}-\color{magenta}{AE}}\)
\(\mathrm{FO=\color{red}{CO}-\color{magenta}{CF}}\)
仮定から\(\,\mathrm{\color{magenta}{AE}=\color{magenta}{CF}}\,\)であるから①と合わると
\(\,\mathrm{EO=FO} ･･･③\,\)
②③から対角線がそれぞれの中点で交わっていることを示しているので
四角形\(\,\mathrm{EBFD}\,\)は平行四辺形である。（終わり）
平行四辺形の成立条件で\(\,7\,\)点って、ありがたいですね。
\(\large{\,3\,}\),\(\large{\,4\,}\)もここで解説しようと考えましたが学校選択問題と同じなので別にします。
⇒ 2019年度埼玉県公立高校入試数学第3問4問(同学校選択問題)の解説
\(\large{3}\)は関数の面積問題です。
三角形の面積を求める簡単な問題と座標設定のちょっとした応用ですね。
⇒ 2019年(平成31年)度埼玉県公立高校入試数学の問題と解説
\(\large{\,1\,}\) と \(\large{\,2\,}\) で\(73\)点です。
⇒ 埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策
2018年度と合わせて何が大切かを理解しておくと良いです。