埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策

埼玉県公立高校入試（平成30年度）の数学過去問題のここでしか見られないオリジナル解説です。
数学だけになりますが、特別対策付きのこの解説は永久保存版にしても良いくらい価値があります。
特に、過去問を解いていて「平均点いきそうもない」、と悩んでいる方には必見です。

※（依頼人です。）
この記事は、このサイトで取り上げている科学的なことでは、いつも相談に乗ってもらっている科学者の方にお願いして書いていただきました。
実は、友人のお子さんが高校受験を控えているのですが、どうしても平均点を取れないと悩んでいるお母さんの様子をみて、現在は受験個別指導のプロとして全国で活躍されている方なので、OKはもらえないかもしれないとダメ元でお願いしたら、『良いよ』、と快く引きくけてくださいました。
私が内容を完全にお伝えできるかわかりませんが、できるだけ忠実にお伝えしますね。

あなたはこの解説を読んで、「そんなこと知ってるよ」といえますか？
私も過去にいろいろな塾に息子を通わせたけど、このような解説は聞いたことがありません。
また、何冊も問題集を買いましたがここまでの解説はみたことありませんよ。
全国の公立入試や大学入試でも通用する対策方法だそうです。
息子の受験のときにあれば、もう少し楽な気持ちでいられたかもしれません。笑

では、超強力な解説と対策をご覧下さい。

埼玉県公立高校数学平成30年度過去問の解き方と解説

問題は埼玉県立総合教育センターにもあります。

⇒　2018埼玉県立高等学校入試問題

最初にお伝えしておきます。

　\(\large{\color{magenta}{\fbox{平均点：44.0}}}\)

これは信じられない、というか普通に対策すればあり得ない数字です。
現時点で平均点がとれないと感じる人は、
教科書程度の基礎問題だけで必ず到達できるようになりますので絶対にあきらめないでください。

ただし、ここでする解説は時間の限られる、1回限りの説明になるのであまり期待しないで下さい。
何でもそうですが、期待するとろくなことはありません。笑

※（依頼人の注釈）
途中で余計な説明入れてすみません。
「塾に行っていて平均点を目標にしているお友達へのプレゼントでしょう？
大きな声では言えませんが、その塾やめた方が良いですよ。」
とおっしゃっていました。笑
模擬試験などで生徒に普通に満点取らせる方なので、効果の出ない「親の気休め塾通い」が嫌いな方です。

第1問（小問集合）の解説

文字式の足し算

(1)　\(4x+x\)　を計算しなさい。

普通に同類項をまとめるだけですね。
係数の足し算になりますが、\(x\) という項には係数1が省略されていることを忘れないようにしましょう。

　\(4x+x=(4+1)x=\underline{5x}\)

加減乗除の優先順位

(2)　\(6-4\div(-2)\)　を計算しなさい。

ここは算数と同じで計算順序を間違えないようにしましょう。
かけ算や割り算は、足し算や引き算より先です。

　\(6-4\div(-2)\\ \\
=6-\{4\div (-2)\}\\ \\
=6-(-2)\\ \\
=6+2=\underline{8}\)

私の生徒のように割り算を逆数のかけ算とすることをクセづけている人は、違った方法になりますがどちらでも良いです。

　\(6-4\div(-2)\\ \\
\displaystyle =6-4\times \left(-\frac{1}{2}\right)\\ \\
=6+2=\underline{8}\)

文字式の乗法除法

(3)　\(16a^2b\div (-8b)\times a\)　を計算しなさい。

文字式の計算です。
これも習った方法によって違う計算方法になりますが、どちらでも良いです。
かけ算割り算だけなので順番に計算します。

　\(16a^2b\div (-8b)\times a\\ \\
=-2a^2\times a\\ \\
=\underline{-2a^3}\)

割り算は逆数のかけ算としている人は、

　\(16a^2b\div (-8b)\times a\\ \\
\displaystyle =\frac{\color{red}{16}a^2\color{blue}{b}\times a}{-\color{red}{8}\color{blue}{b}}　←（\color{red}{約分利用}）\\ \\
=-2a^2\times a\\ \\
=\underline{-2a^3}\)

この程度の文字式だと差は出ませんが、
文字式がたくさんある場合は分数にするとすべて同じ方法で短時間で終わります。

符号（＋や－）には気をつけておきましょう。

無理数の有理化と減法

(4)　\(\displaystyle \frac{9}{\sqrt{3}}-2\sqrt{3}\)　を計算しなさい。

無理数の計算確認問題ですが分母の有理化と足し算です。

分母の有理化の説明は必要はないと思いますが、ていねいにやっておきます。

　\(\displaystyle \frac{9}{\sqrt{3}}-2\sqrt{3}\\ \\
\displaystyle =\frac{9\times \color{red}{\sqrt{3}}}{\sqrt{3}\times \color{red}{\sqrt{3}}}-2\sqrt{3}　←（\color{red}{有理化です}）\\ \\
\displaystyle =\frac{\color{blue}{9}\times \sqrt{3}}{\color{blue}{3}}-2\sqrt{3}　←（\color{blue}{約分です}）\\ \\
=\color{magenta}{3}\sqrt{3}-\color{magenta}{2}\sqrt{3}　←（ルートの中が同じなので整数部分の引き算）\\ \\
=\underline{\sqrt{3}}\)　

問題の最初のページに書いてありますが、無理数はそのままで良いとあります。
普通は近似しませんので問題に書いていなくても無理数のままで良いですよ。
ただし、分母の無理数は有理化するように指示されます。

因数分解の注目ポイント

(5)　\(x^2+x-12\)　を因数分解しなさい。

因数分解の第一歩は共通因数の抜き出しですがありませんので、
定数項の　\(-12\)　と \(x\) の1次の項の係数　\(+1\)　に着目します。

かけて　\(12\)　となり、
足し足り引いたりして　\(+1\)　となる組み合わせを探します。

かけて　\(12\)　となるのは
　\(\color{black}{\fbox{1 × 12}}\) 　\(\color{black}{\fbox{2 × 6}}\) 　\(\color{red}{\fbox{3 × 4}}\)
後は逆になるだけなのでこの組み合わせだけで良いです。
定数項は-12なのでどちらかに「－」をつけて、加えると＋1になるのは、
　\(\color{red}{\fbox{(-3) × 4}}\)　です。

だから
　\(x^2+x-12=\underline{(x-3)(x+4)}\)

問題に「因数分解しなさい。」とあれば必ず因数分解できます。
因数分解した後、展開して問題と同じ式になれば正解です。

連立方程式を代入法で解くときの計算ミスを減らすコツ

(6)　連立方程式　\( \begin{cases}
2x-3y=11\\
y=x-4\\
\end{cases}\)　を解きなさい。

連立方程式の解き方の基本は一文字消去です。

　\(y=x-4\)　を　\(-x+y=-4\)　として、
加減法も使えますがここでは代入法が早いでしょう。

　\( \begin{cases}
2x-3y=11\\
y=x-4\\
\end{cases}\)

　\( 2x-3y=11\)　の \(y\) に　\(y=\color{red}{x-4}\)　を代入します。
代入するときのポイントは符号に関係なく（かっこ）をつけることですが、ここの読者にはお伝えしていませんね。

代入するときはかっこつけるとミスが減ります。

　\(\begin{eqnarray}
2x-3y&=&11\\
2x-3\color{red}{(x-4)}&=&11　（代入）\\
2x-3x\color{red}{+12}&=&11　（符号注意）\\
2x-3x&=&11\color{red}{-12}　（移項）\\
-x&=&-1\\
x&=&1
\end{eqnarray}\)

ここで終わったらダメですよ。
「連立方程式を解きなさい。」なので　\(y\)　も求めます。
（解答用紙にあるので忘れることはないでしょうけど。）

　\(y=x-4\)　に　\(x=1\)　を代入するのが早いでしょう。

　\(y=x-4\\
=(1)-4\\
=1-4\\
=-3\)

答え　\(\underline{x=1\,,\,y=-3}\)

２次方程式の解き方順序と解の公式

(7)　\(3x^2-x-1=0\)　を解きなさい。

「方程式を解きなさい。」ということは、
その方程式を満たす \(x\) を求めなさい、ということです。
方程式の解とはその方程式を満たすもののことなので、
「方程式の解を求めなさい。」と同じです。

２次方程式を解くときは因数分解を利用するのが優先ですが、
この２次方程式は因数分解できません。

解の公式の確認問題です。

２次方程式　\(ax^2+bx+c=0\)　の解は
　\(\large{\displaystyle \color{red}{x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}}} \)
導き方はいくつかありますが、覚えた方がはやいです。
試験中に導くには試験時間がもったいない。

覚え方は簡単です。
解の公式を声に出して１０回唱える、それを数日間やってください。
　『エックスイコール・2a分の・マイナスbプラスマイナスルートbの2乗マイナス4ac』
勝手に口が覚えてくれます。

　\(3x^2-x-1=0\)　は
　\(\color{red}{a=3}\,,\,\color{blue}{b=-1}\,,\,\color{magenta}{c=-1}\)　
なので、これらを解の公式に代入していきます。

　\(\displaystyle x=\frac{-(\color{blue}{-1})\pm \sqrt{(\color{blue}{-1})^2-4\cdot (\color{red}{3})\cdot (\color{magenta}{-1})}}{2\times \color{red}{3}}\\
\displaystyle =\frac{1\pm \sqrt{1+12}}{6}\\
\displaystyle =\frac{1\pm \sqrt{13}}{6}　（答え）\)　

2乗に比例する関数の比例定数の決定と思い込み注意点

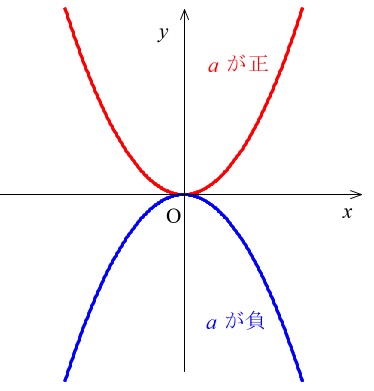
(8)　関数 \(y=ax^2\)　について，\(x\) の変域が　\(-1≦x≦2\)　のとき，\(y\) の変域は　\(－8≦y≦0\)　となりました。このとき，\(a\) の値を求めなさい。

2次関数、放物線の問題です。
関数の問題に取り組むときはグラフをできるだけ書くことです。
関数全体ではもっとやることはありますが、後の問題にありますのでそこで説明します。

　\(y=ax^2\)　のグラフは \(a\) が正のときと負のときで形が上下逆になります。

　\(a\) が正のときは下に凸（上に開く）形
　\(a\) が負のときは上に凸（下に開く）形

になります。

　\(y\) の変域は　\(\color{red}{－8≦y≦0}\)

となるとすれば \(a\) は負のときしかあり得ません。

ここで利用できるのが埼玉県の場合は「別紙」です。
解答用紙と別に計算用紙として別紙が配られますので、その紙に大まかなグラフを書いてみるとすぐにわかります。

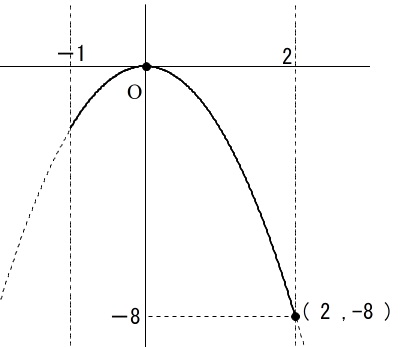
　\(x\) の変域が　\(-1≦x≦2\)　のとき，\(y\) の変域は　\(－8≦y≦0\)

をグラフにすると、\(y=ax^2\) のグラフは \(y\) 軸を軸として左右対称なので

これから \(x=2\) のときに \(y=-8\) となるはずです。
（原点が最大で \(x=-1\) のときは最大、最小に関係がない。）

　\(y=ax^2\) の比例定数は原点以外の1点を代入すれば決まるので、
\((\,x\,,\,y\,)=(\,2\,,\,-8\,)\)　を　\(y=ax^2\)　に代入して、

　\(-8=a(2)^2=4a\)　これから　\(\underline{a=-2}\)　

関数では思い込みは禁物ですので、できるだけグラフは書いて考えるようにしましょう。

　\(y=ax^2\)　の関数でも比例や反比例と同じで\(\color{red}{定数 a}\) を比例定数というのは確認しておいてください。

移項とは何か覚えていますか

(9)　方程式 \(3(2x-1)=-9\) を，次のように解きました。「等式の両辺に同じ数をたしても，等式は成り立つ。」という等式の性質を使って，方程式を変形しているのはどこですか。ア～エの中から1つ選び，その記号を書きなさい。

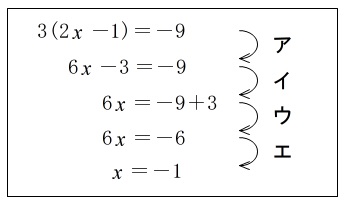
この問題の『「等式の両辺に同じ数をたしても，等式は成り立つ。」という等式の性質を使って，方程式を変形』は、『移項』のことです。
移項についてはすでに（6）で説明しているので必要ありませんが、再度説明しておきます。

　方程式 \(3(2x-1)=-9\)　を解くときに、展開して \(x\) の項だけを左辺に残すように変形します。

　\(\begin{eqnarray}
3(2x-1)&=&-9\\
6x-3&=&-9
\end{eqnarray}\)

ここで－3を右辺に移項したいのですが、符号を変えて右辺に移項するのが普通になっていると思いますが、これは両辺に＋3をたしているのと同じことです。

　　\(\begin{eqnarray}
3(2x-1)&=&-9\\
6x-3&=&-9\\
6x-3\color{red}{+3}&=&-9\color{red}{+3}\\
6x&=&-9+3\\
6x&=&-6\\
x&=&-1
\end{eqnarray}\)

この3行目を省略しても問題はありません。
ただ、ここで聞いているのは、「移項すると符号が変わる意味を思い出してください。」ということです。

答えは　\(\underline{イ}\)

移項は両辺に等しい数を加えていることになります。

一方で係数を1に変えるときや分母を無くすときなどは両辺に同じ数をかけています。

　\(\begin{eqnarray}
6x&=&-6\\
x&=&-1
\end{eqnarray}\)

これは

　\(\begin{eqnarray}
6x&=&-6\\
6x\times \color{red}{\frac{1}{6}}&=&-6\times \color{red}{\frac{1}{6}}\\
x&=&-1
\end{eqnarray}\)

こういう基本的な操作の意味を問う問題構成はなかなか面白いですね。
答えは出せる、でも機械的、という人が多いですから。

度数分布表から平均値を出す方法

(10)　

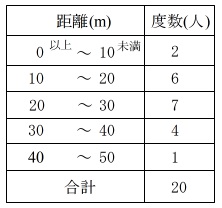右の表は，あるクラスのハンドボール投げの記録を，度数分布表に表したものです。このクラスのハンドボール投げの記録の平均値を，度数分布表から求めなさい。

求めるものは平均値です。
平均値は総得点を総人数で割ったものになります。

　\(\displaystyle \color{red}{平均値＝\frac{総得点}{度数合計}}\)

ただ、総得点が度数分布表でははっきりしません。
例えば、階級\(\,10\,\mathrm{m}以上\,20\,\mathrm{m}未満\)には6人いますが、この6人の距離はそれぞれ何mなのかわかっていません。

そこで、度数分布表で表された場合は、
その階級の人全員が階級の真ん中の値と見なします。

この階級の真ん中の値を『階級値』といいます。
階級\(\,10\,\mathrm{m}以上\,20\,\mathrm{m}未満\)の階級値は \(15\,\mathrm{m}\)です。
階級\(\,20\,\mathrm{m}以上\,30\,\mathrm{m}未満\)の階級値は \(25\,\mathrm{m}\)です。

階級値の求め方は階級の左端（小さい値）と右端（大きい値）をたして2で割れば出てきます。

　\(\displaystyle 階級値＝\frac{階級の左端＋右端}{2}\)

階級値に度数をかけて、すべてたすと総得点となります。

　階級値　 5m　の人は　\(\color{red}{2}\)人
　階級値　15m　の人は　\(\color{red}{6}\)人
　階級値　25m　の人は　\(\color{red}{7}\)人
　階級値　35m　の人は　\(\color{red}{4}\)人
　階級値　45m　の人は　\(\color{red}{1}\)人

平均値は　\(\displaystyle \frac{　(階級値×度数)の和　}{度数合計}\)
なので平均値は
　
　\(\displaystyle \frac{5\times 2+15\times 6+25\times 7+35\times 4+45\times 1}{20}\\
\displaystyle =\frac{10+90+175+140+45}{20}\\
\displaystyle =\frac{460}{20}\\
=23\)

説明が長かったですが、度数分布表では階級値を採用するとわかっていれば、
この問題は最後の計算だけで答えが出ます。

これは問題用紙のあいている部分で計算できる程度の量です。

食塩水を混合するときのポイント

(11)　濃度が，6％の食塩水と10％の食塩水があります。この2種類の食塩水を混ぜ合わせて，7％の食塩水を600gつくります。次の①，②に答えなさい。
（ビーカーで混ぜている絵がありますが問題に関係ないので省略します。）
①7％の食塩水600gに含まれる食塩の質量を求めなさい。
②6％の食塩水を \(x\) g，10％の食塩水を \(y\) gとして，連立方程式をつくり，6％の食塩水と10％の食塩水の質量をそれぞれ求めなさい。
なお、考えるときに、下の表を利用してもさしつかえありません。

	6％の食塩水	10％の食塩水	7％の食塩水
食塩水の質量(g)	\(x\)	\(y\)
食塩の割合
食塩の質量(g)

食塩水の問題ではポイントがいくつかあります。

１つは溶液とは「溶媒＋溶質」であること。
つまり、
　\(\color{magenta}{\fbox{食塩水＝水＋食塩}}\)
であることです。

もう一つは濃度、
　\(\displaystyle \color{red}{濃度(％)＝\frac{食塩}{食塩水}　\times 100(％)}\)

この食塩水は水と食塩が混じったものですが、
食塩水の問題を解くときの基本としては、水に関して方程式を立てるということはしません。

加えた水の量を文字でおくことはありますが方程式自体は、
　\(\color{red}{\fbox{溶液の量}}\)
　\(\color{magenta}{\fbox{食塩の量}}\)
この２つについて方程式を立てていくとほとんどがうまくいきます。

この２つを追いながら方程式を立てて見ましょう。

溶液について成り立つ関係式は、
　『　6％の食塩水と10％の食塩水があります。
　この2種類の食塩水を混ぜ合わせて，7％の食塩水を600g　』　
という問題文から、
　6％の食塩水の量を \(x \,\mathrm{g}\)
　10％の食塩水の量を \(y \,\mathrm{g}\)
とすると、混ぜ合わせた後は600gになるので、
　\(x+y=600　･･･(ア)\)

食塩の量は％で表されているので、
　6％の食塩水　\(100\,\mathrm{g}中に\,6\,\mathrm{g}\)
　10％の食塩水　\(100\,\mathrm{g}中に\,10\,\mathrm{g}\)
の食塩が含まれていることになります。

同じ濃度の食塩水では、食塩水が多くなればその中に含まれる食塩の量も増えます。
つまり、食塩水の量とその中に含まれる食塩の量は比例するので、
6％の食塩水 \(x \,\mathrm{g}\)中だと何gあるかは比例式で求まります。
　\(x \,\mathrm{g}\) 中に \(a\,\mathrm{g}\) あるとすると、

　\(100\,\mathrm{g}\)の食塩水中に\(6\,\mathrm{g}\)の食塩なら、
　\(x \,\mathrm{g}\) の食塩水中に \(a\,\mathrm{g}\)の食塩、
という比例なので

　\(\begin{eqnarray}
100：6&=&x:a\\
100a&=&6x\\
\displaystyle a&=&\frac{6x}{100}
\end{eqnarray}\)

これが \(6\) ％の食塩水 \(x \,\mathrm{g}\) 中の食塩の量です。

同じように \(10\) ％の食塩水 \(y \,\mathrm{g}\) 中の食塩の量は
　\(\displaystyle \frac{10y}{100}\)
となります。

食塩水を混ぜ合わせた後の食塩の量はこの2つの和になります。
たとえ水を蒸発させたとしても食塩の量は変わりません。
しかもここでは混ぜただけなので単なる「和」です。

さて、前置きが長くなりましたが問題を解いてみましょう。

①7％の食塩水600gに含まれる食塩の質量を求めなさい。

\(7\) ％の食塩水は \(100\, \mathrm{g}\) の食塩水（溶液中）に \(7\,\mathrm{g}\) の食塩（溶質）を含んでいます。
だから \(600\,\mathrm{g}\) 中に \(m\,\mathrm{g}\) 含まれているとすると、

　\(\begin{eqnarray}
100:7&=&600:m\\
100\,m&=&7\times 600\\
100\,m&=&4200\\
m&=&\underline{42}
\end{eqnarray}\)

比例式で解いてみればすぐに出ます。

しかし、比例関係の作り方を知っている私の生徒は、
　\(\displaystyle 7\times \frac{600}{100}=\underline{42}\)
と瞬間で答えを出してしまいますが学校で教わった方法でかまいません。
もちろん、基本的には比例関係なので比例式です。

②6％の食塩水を \(x\) g，10％の食塩水を \(y\) gとして，連立方程式をつくり，6％の食塩水と10％の食塩水の質量をそれぞれ求めなさい。
なお、考えるときに、下の表を利用してもさしつかえありません。

②のこの部分単独では解くことはできません。
問題文全体から連立方程式を立てます。

①はなくてもおかしくない問題ですが、①はヒントとして出題してくれています。
こういう問題構成を誘導といいます。

問題文全体を見ると

　\(\color{black}{\fbox{濃度が，6％の食塩水と10％の食塩水があります。}}\)
　\(\color{black}{\fbox{混ぜ合わせて，7％の食塩水を600gつくります。}}\)

この条件から \(x\) と \(y\) の2つを求めます。
文字2つなので方程式が2つあれば良いのですが、

　\(\color{magenta}{\fbox{食塩水の量}}\)
　\(\color{red}{\fbox{食塩の量}}\)

についての方程式を立てます。

食塩水の量については、
　2つの食塩水をたして600g
これは問題に入る前に出している式です。

　\(x+y=600　･･･(ア)\)

食塩の量については、
　6％の食塩水 \(x\) g中の食塩と、
　10％の食塩水 \(y\) g中の食塩とをたすと、
　7％の食塩水 \(600\) g中の食塩
になっているはずです。
食塩は混ぜても消えないので、元の量の和になっていないとおかしいです。

　6％の食塩水 \(x\) g中の食塩の量 \(a\) は、
比例式
　\(100:6=x:a\)　から \(\displaystyle a=\frac{6x}{100}　\)

　10％の食塩水 \(y\) g中の食塩の量 \(b\) は、
比例式
　\(100:10=y:b\)　から \(\displaystyle b=\frac{10y}{100}　\)

7％の食塩水 \(600\) g中の食塩の量は①で \(42\,\mathrm{g}\) と求めているので使いましょう。

すると、\(a+b=42\) になります。
これを \(x\,,\,y\) の方程式にすると、
　\(\displaystyle \frac{6x}{100}+\frac{10x}{100}=42　･･･(イ)\)

（解答には \(a\,,\,b\) の式は必要ありません。）

せっかく表を与えてくれているので使ってみましょう。
　

	6％の食塩水	10％の食塩水	7％の食塩水
食塩水の質量(g)	\(x\)	\(y\)	\(600\)
食塩の割合	\(\displaystyle \frac{6}{100}\)	\(\displaystyle \frac{10}{100}\)	\(\displaystyle \frac{7}{100}\)
食塩の質量(g)	\(\displaystyle \frac{6}{100}\times x\)	\(\displaystyle \frac{10}{100}\times y\)	\(\displaystyle \frac{7}{100}\times 600\)

割合は小数でも良いですが、分数の方が計算処理するときに早い場合が多いです。

表がなくても連立方程式は立てられますが、
　表の食塩水の質量と、食塩の割合を、かけると食塩の量になっている
ということには気がついて下さい。
連立方程式は

　\( \begin{cases}
\hspace{7pt} x+y=600\hspace{30pt}･･･(ア)\\ \\
\hspace{7pt} \displaystyle \frac{6x}{100}+\frac{10y}{100}=42\hspace{10pt}･･･(イ)
\end{cases}\)

となります。
下の方程式は①がなければ
　\(\displaystyle \frac{6x}{100}+\frac{10y}{100}=\frac{7}{100}\times 600\)
とするところですが①で右辺は求めているので利用した形で表しました。

約分はしてもしなくても減点はないといえるでしょう。
逆に約分していると式の意味がわかりにくいですからね。

この連立方程式を解きます。
下の方程式（イ）は両辺100倍して、係数を簡単な小さい整数に変形すると
　
　\(\begin{eqnarray}
\displaystyle \frac{6x}{100}+\frac{10y}{100}&=&42\\
6\,x\,+\,10\,y&=&4200\\
3\,x\,+\,5\,y&=&2100　･･･(イ)’
\end{eqnarray}\)

これと（ア）から加減法で解きます。
\(（ア）\times 3\) から
　\(3\,x\,+\,3\,y=1800　･･･(ア)’\)

　\(3\,x\,+\,5\,y=2100　･･･(イ)’\)
と
　\(3\,x\,+\,3\,y=1800　･･･(ア)’\)
から　\(x\)　を消去して、
　\(2\,y=300\)　よって　\(y=150\)

このとき　\(x+y=600\)　から　\(x=450\)

答えは連立方程式と食塩水の量をそれぞれ答えることになっています。

(答え）
連立方程式
　　\( \begin{cases}
\hspace{7pt} x+y=600\hspace{30pt}\\ \\
\hspace{7pt} \displaystyle \frac{6x}{100}+\frac{10y}{100}=42\hspace{10pt}
\end{cases}\)

6％の食塩水　\(450\,\mathrm{g}\)
10％の食塩水　\(150\,\mathrm{g}\)