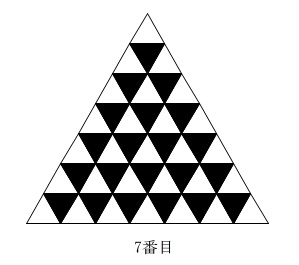
公立高校入試過去問から規則性の問題を攻略する方法です。
問題は埼玉県立公立高校入試の平成30年度の第3問を取り上げています。
規則性の問題は決まった公式がありませんので、苦手にしている人が多いですが小学生でもできる問題はあります。
数学の始まりといってもいい分野なので楽しめる分野でもあるので、確認してみて下さい。
※(依頼人です。)
第3弾お待たせしました。
第3問目の規則性の問題のオリジナル解説と対策です。
小学生でもできる問題があるということ、楽しめる分野だということなので、ここでうっかりミスをしないようにして加点していきましょう。
私でも図に書いてやってみたら出来ました!
おばさんにも分かったんだから、頭の柔軟な中学生だったら大丈夫ですね。
では、超強力な解説と対策をご覧下さい。
問題は埼玉県立総合教育センターにもあります。
第3問 規則性と文字式の利用(これが数学の始まりです)
3 下の図のように,同じ大きさの正三角形の白いタイルと黒いタイルをすき間なくしきつめて,
1番目,2番目,3番目,4番目,・・・・・・,\(n\) 番目までの正三角形をつくります。
このとき,次の問いに答えなさい。
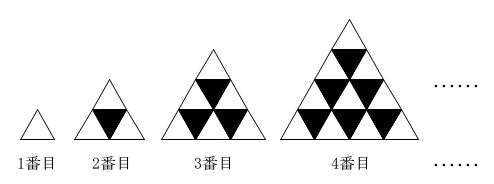
これが第3問のすべてに通じる条件です。
これから読み取れることはたくさんありますが、やみくもに進めても時間がかかるので問題の指示に従いましょう。
問題の順番通りに解いて、次の問題に利用して行くことを誘導に乗る、といいますが大学入試でも変わりません。
高校入試でも小問集合以外は誘導してくれていると思って間違いないですよ。
もちろん、誘導に乗らなくても答えは出せます。
数学の解法は1つではありませんからいろいろな方法で答えは出てきます。
しかし、そういったレベルになるにはかなりの練習量が必要になるし、受験までにはなかなか到達できません。
だから誘導に乗ってやるべきことをやれば高校入試の問題も解けるようにつくられているのです。
埼玉県の問題をつくられている方々はかなり親切ですよ。
この問題はよくある形なのでおおよそ予想はできますが、手をつける前に問題に入りましょう。
小学生でもできる規則性の読み取り
(1)下の表は,1番目,2番目,3番目,4番目,・・・・・・,\(n\) 番目までの正三角形をつくるに必要な
白いタイルと黒いタイルの枚数についてまとめたものです。\(\color{black}{\fbox{ ア }}\) と \(\color{black}{\fbox{ イ }}\) にあてはまる数をそれぞれ書きなさい。
| 1 | 2 | 3 | 4 | \(\cdots\) | 7 | \(\cdots\) | \(n\) | |
| 白いタイル(枚) | 1 | 3 | 6 | 10 | \(\cdots\) | \(\color{black}{\fbox{ア}}\) | \(\cdots\) | |
| 黒いタイル(枚) | 0 | 1 | 3 | 6 | \(\cdots\) | \(\color{black}{\fbox{イ}}\) | \(\cdots\) | |
| タイルの合計(枚) | 1 | 4 | 9 | 16 | \(\cdots\) | \(\cdots\) |
数字に慣れていれば数字だけを見てても答えは出ます。
この(1)は小学生でも読み取れるのでちょっと数字だけでも追いかけてみましょう。
白いタイルの枚数は1番目から順に4番目まで
\(1\,,\,3\,,\,6\,,\,10\,,\,\cdots \)
となっています。
では、5番目は?
予想でも良いんです。
\(15\) 正解です。
1番目から2番目になるときタイルは \(2\) 増えています。
2番目から3番目になるときタイルは \(3\) 増えています。
3番目から4番目になるときタイルは \(4\) 増えています。
4番目から5番目になるときタイルは \(5\) 増えそうです。
だから、順に見て7番目の白いタイルの枚数は
\(1\,,\,3\,,\,6\,,\,10\,,\,15\,,\,21\,,\,\color{magenta}{\fbox{28}}\,,\,36\,,\cdots\)
となると予想できます。
「予想で答えて良いのですか?」
ダメです。笑
でも答えは出ています。
同じように黒いタイルも
\(0\,,\,1\,,\,3\,,\,6\,,\,10\,,\,15\,,\,\color{red}{\fbox{21}}\,,\,28\,,\,\cdots\)
根拠が欲しいですよね?
簡単です。図を書いていけば良いだけです。
順番に7番目までの図を書いていけば必ずわかります。
小学生でもできることをなぜ中学生や高校生はやらないのか不思議です。
何でも数式で出さなければダメなんて考えているのでしょうか?
この規則性を見るというのは数学の始まりと言っても良いくらいのものです。
それを一般化してきたのが現代にある数学ですよ。
7番目の図は順番に書いていけば出てきますが、
一番下に白いタイルが7個並ぶんですよね?
数えました?
白いタイルは \(\color{magenta}{\fbox{28}}\) 枚
黒いタイルは \(\color{red}{\fbox{21}}\) 枚
で間違いありません。
答え \(\color{black}{\fbox{ア}}\):28 \(\color{black}{\fbox{イ}}\):21
これが、この小学生でも出せる答えが4点になります。
よく見ると数学的に見せることができる
一般的な数字 \(n\) を用いて表す問題は数列という高校の数学の土台になります。
ただ、高校入試での規則性は高校であつかう数列ほどややこしくはありません。
何かしらのセットがあるのです。
この問題では縦に見ても、横に見ても良いですが、
前の正三角形に、何かを継ぎ足していっているのはわかりますよね?
この増え方が見えるようになるとほとんどの規則性の問題は解けます。
ここでは、すべてに通じる方法を説明する時間がないのでこの問題に合わせた考え方をお伝えします。
(2) \(n\) 番目の正三角形をつくるのに必要な黒いタイルの枚数を \(a\) 枚とするとき,\(a\) を \(n\) を使った式で表しなさい。
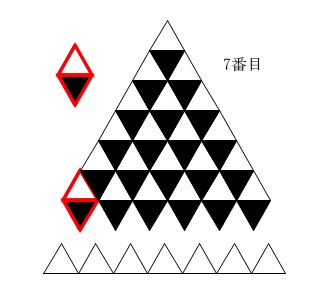
7番目の図で良いので確認して欲しいのですが、一番下には白いタイルが7枚あります。
その上に白と黒のタイルを2つくっつけたひし形が並んでいるのがわかりますか?
白いタイルを取ってしまうとよくわかります。
まずはこのセットがいくつあるか文字で表して見ましょう。
それが黒いタイルの枚数です。
タイル枚数を表した表を見直して下さい。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | \(\cdots\) | \(n\) | |
| 白いタイル(枚) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | \(\cdots\) | |
| 黒いタイル(枚) | 0 | 1 | 3 | 6 | 10 | 16 | 21 | \(\cdots\) | |
| タイルの合計(枚) | 1 | 4 | 9 | 16 | 25 | 36 | 49 | \(\cdots\) | \(n^2\) |
見て欲しいのはタイルの合計枚数です。
\(\hspace{10pt} 1 , 4 , 9 , 16 , \cdots , \color{red}{n 枚目の合計}\)
\(\rightarrow 1^2 , 2^2 , 3^2 , 4^2 , \cdots , \color{red}{n^2}\)
このように \(n\) 番目はタイル合計が \(n^2\) になっています。
ところで積まれた正三角形の一番下の白いタイルは、
1番目から1,2,3,4,・・・ 枚、
\(n\) 番目には \(n\) 枚あります。
合計枚数からこの一番下の白いタイルを取るとひし形をつくっている個数となります。
文字式で表すと、
\(\color{red}{ひし形をつくっている合計数=n^2-n}\)
このひし形は白いタイルと黒いタイルと一枚ずつでできているので、
ひし形の数、つまり黒いタイルの枚数 \(a\) はその半分になります。
\(\displaystyle a=\frac{n^2-n}{2}\)
このような問題は結構楽しいのでもう少し見ておきましょうか。
方法はいろいろあるんですけど、
例えば、7番目の大きな正三角形をもう一つ用意して、ひっくり返してくっつけてみます。

このままでは見にくいので、右上にひっつけた正三角形の白黒をひっくり返してみましょう。

これは大きな正三角形2つ分なので、
タイルの合計枚数は \(2n^2\) 枚あります。
ここからが面白い。
上の白い部分を取ってしまいましょう。
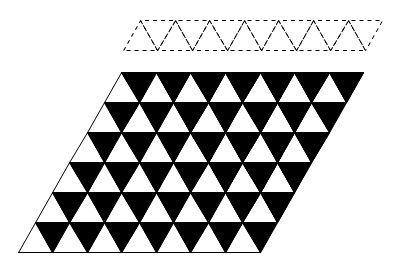
取ってしまった点線部分の△は \(n\) 番目だと \(2n\) 個あります。
すると下の平行四辺形にある△の総数は
\(2n^2-2n\) 個になります。
これは元の大きな正三角形2つ分なので1つ分だとその半分で
\(\displaystyle \frac{2n^2-2n}{2}=n^2-n\)
そして残りの下の平行四辺形の中には、白と黒のタイルが同じ枚数あります。
だから \(n\) 番目の黒のタイル数 \(a\) は
\(\displaystyle a=\frac{n^2-n}{2}\)
他にも組み方はいろいろあるのでやってみて下さい。
数学は答えは同じでも、解き方は1つではありません。
だからあまり堅苦しく考えずに数学に取り組んでみて下さい。
これを見ているのがお父様やお母様なら、
お子様にもっと数学を楽しむように勧めてやって下さい。
きっと反抗期で、
「全・然・楽しくないし!」
とか言われるのでしょう。笑
でもですね、それは教え方が悪いだけでお子様が悪いのではないということを理解しておいて下さいね。
じっくり考えれば割と楽しいんですよ。
将来役に立たない、という人はやってみて本当に役に立たないか知ってからいって下さい。
受験のための勉強は面白くない、というのは事実ですけどね。笑
それすら楽しめたら最高ですよね。
ということで最後の第4問です。
関数は簡単です。
※(依頼人です。)
いかがでしたか?
「全・然・楽しくないし!」とお子さんは言ったでしょうか?
「解けた、これ簡単だったし!」と言ってくれたらそれだけで親はちょっとホッとしますよね。
嬉しいことに最後の第4問目は簡単だと先生は言われているので、目の前に明るい日差しが見えてきそうと思われている方も多いでしょう。
友人の笑っている顔も目に浮かびます。
その4問目も頑張って近日公開致しますのでもう少しお待ちくださいね。
⇒ 埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策
埼玉県公立高校入試(平成30年度)の第1問目のオリジナル解説と対策になります。
⇒ 埼玉県立高校入試(2018過去問) 確率と図形問題の解説とポイント
埼玉県公立高校入試(平成30年度)の第2問目のオリジナル解説と対策になります。
⇒ 埼玉県公立入試2018の過去問で差がつく関数問題の解き方がわかる
埼玉県公立入試2018数学過去問の4問目は関数問題です。
こちらの最終問題もオリジナル解説と対策をお伝えしています。
⇒ 2019年(平成31年)度埼玉県公立高校入試数学の問題と解説
\(2019\)年の問題も詳しく解説をお伝えしていますので見ておくと良いです。
⇒受験生が食事からとるべき栄養と時間帯 前日と当日の朝や弁当はどうする?
受験生にとって、前日や当日に食事も重要なのです。
⇒ 2019年度全国の公立高校入試の一般入試日程と合格発表日一覧
今年の入試日程と合格発表日をこちらで確認できます。