埼玉県公立入試2018の過去問で差がつく関数問題の解き方がわかる

埼玉県立高校入試2018年の数学の過去問解説です。
第4問関数の解説ですが、この問題からも関数全体でのコツをつかむことができます。
関数を苦手にしている人は何を間違えているのでしょうか。
何が足りていないのでしょうか。
高得点を取る人との違いはちょっとしたポイントだけでした。

※（依頼人です。）
第4弾お待たせしました。
埼玉県公立高校入試2018年数学の過去問題4問目のオリジナル解説と対策です。

この解説でコツをつかんで今までの苦手意識を過去のものにしましょう！

では、今回で数学の過去問最後となる超強力な解説と対策をご覧下さい。

問題は埼玉県立総合教育センターにもあります。

⇒　2018埼玉県立高等学校入試問題

関数はたった4つしかない

高校受験の数学の中で関数と呼ばれるものはたった4つしかありません。

　比例　\(y=ax\)
　反比例　\(\displaystyle y=\frac{a}{x}\)
　１次関数　\(y=ax+b\)
　２次関数　\(y=ax^2\)

この４つしかありません。
しかも、比例は１次関数の１つだし、２次関数は原点を通る場合しかやりません。

覚えておかないといけないこともありますけど、
最低限のことを覚えればたいしたことはありませんよ。

平均点以上とれれば良いなら面積がからんでくる応用問題は捨てても良いですけど、
基本問題だけでも点数取っておきましょう。

第4問　関数と面積

関数の問題ですが、(1)は小問題集合でも出そうな基本問題です。
(2)もなんだか問題がややこしそうに見えますが普通に答えだけではなくて、「どうやって求めたか書いて下さい。」というのが加わっただけです。
(3)はちょっと考え方を変えれば簡単に答えが出るのですが、途中でやることが多いので後回しでもかまいません。

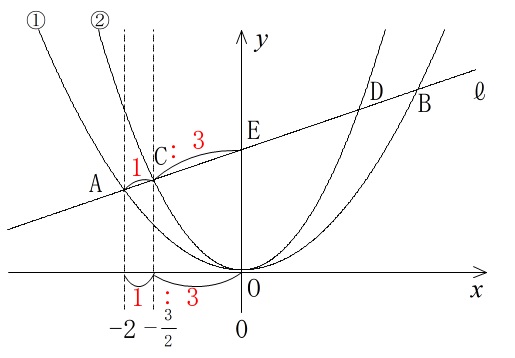
右の図1において，曲線①は関数　\(\displaystyle y=\frac{1}{2}x^2\)

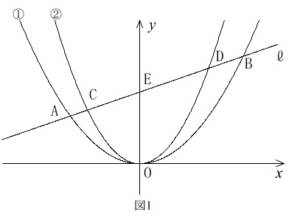
のグラフで，曲線②は関数 \(\displaystyle y=ax^2\,(a>\frac{1}{2})\)
のグラフです。曲線①上に \(x\) 座標が－2，3
である2点A，Bをとり，この2点を通る直線 \(\ell\)
をひきます。直線 \(\ell\) と曲線②との交点のうち
\(x\) 座標が負である点をC，正である点をDとし，
直線 \(\ell\) と \(y\) 軸との交点をEとします。
　AC:CE＝1：3 のとき，次の各問に答えなさい。

問題に入る前にわかることは見やすく書き出して、グラフに書き込んでおきましょう。
文章で書かれた条件はグラフに書き込むと10倍位わかりやすくなります。
この問題は条件が多くてごちゃごちゃしますので、別紙に大きくグラフを書いて座標を書き込むと見やすくなります。
(3)はちょっと大きめのグラフを問題に与えてくれていますが、情報整理をしっかりしないと関数は難しく感じます。

　\(\mathrm{A}\) の \(x\) 座標は \(－2\)　
①の　\(\displaystyle y=\frac{1}{2}x^2\)　上の点なので、
\(x=-2\) を代入して \(\displaystyle y=\frac{1}{2}(-2)^2\,=\,2\)

　\(\mathrm{A}(\,-2\,,\,2\,)\)

　B の \(x\) 座標は \(3\)
①の　\(\displaystyle y=\frac{1}{2}x^2\)上の点なので、
\(x=3\) を代入して \(\displaystyle y=\frac{1}{2}(3)^2=\frac{9}{2}\)

　\(\displaystyle \mathrm{B}\left(\,3\,,\,\frac{9}{2}\,\right)\)

\(\ell\)　はこの2点を通るのですぐに求まりますが、(1)で問題になっているので後でやります。

わかることは点 \(\mathrm{E}\) は \(\ell\) の切片であることと、

　\(\mathrm{AC}:\mathrm{CE}=1:3\)

これも(2)で使うことになっているので、後で使いますが書き出しておきましょう。

直線は2点があれば求めることができる

(1)直線 \(\ell\) の式を求めなさい。

直線が1次関数とは限りません。
　\(x=1\)　や　\(y=2\)　といった定直線と呼ばれるものも直線なので、
「直線＝1次関数」とはなりませんが、この場合は1次関数です。

1次関数は　\(y=ax+b\)　となります。
　\(a\)　は傾き、\(b\)　は切片（\(y\)切片）
です。

1次関数の求め方は、ほとんどの場合、
　\(\color{black}{\fbox{連立方程式を解くか}}\)
　\(\color{red}{\fbox{傾きを先に求めて、後で切片を求めるか}}\)
の二通りありますが、断然傾きを先に求める方法をおすすめします。

なぜかというと、関数のちょっとした応用問題では1次関数をいくつも求めることになりますし、
連立方程式を解くより使い道が多いからです。

では直線　\(\ell\)　を求めましょう。

　\(\displaystyle \mathrm{A}(\,-2\,,\,2\,)\hspace{8pt}\mathrm{B}\left(\,3\,,\,\frac{9}{2}\right)\)

　\(\displaystyle \color{red}{傾き=\frac{ \hspace{6pt}y\,の増分\hspace{10pt} \,}{ \hspace{6pt}x\,の増分\hspace{10pt}}}\)

なのでそれぞれの増分を出しますが、座標を2つ縦に並べて同じ方向にひけば出ます。

　\((\hspace{10pt}\color{red}{-2}\hspace{10pt},\hspace{10pt}\color{red}{2}\hspace{10pt})\)
　\(\displaystyle \left(\hspace{12pt}\,\color{blue}{3}\hspace{10pt},\hspace{8pt}\color{blue}{\frac{9}{2}}\hspace{10pt}\right)\)

このときの注意点はひく方向を変えないことです。
\(x\) の増分で下の座標から上の座標をひいたら、\(y\) の増分も下から上をひきます。

これを間違えると符号が逆になります。

　下から上をひくと決めておけば良いだけです。

\(\color{magenta}{x　の増分}\)は
　\(\color{blue}{3}－(\color{red}{-2})=3+2=5\)

\(\color{magenta}{y　の増分}\)は
　\(\displaystyle \color{blue}{\frac{9}{2}}-\color{red}{2}=\frac{5}{2}\)

よって傾きは
　\(\displaystyle \frac{\frac{5}{2}}{5}=\frac{5}{2}\times \frac{1}{5}=\frac{1}{2}\)

このとき求める1次関数（直線）は
　\(\displaystyle y=\frac{1}{2}x+b\)
とおけます。
この直線は点 A , B を通るのでどちらかを代入すれば \(b\) が決まります。

　\(\mathrm{A}(\,-2\,,\,2\,)\)　を代入しましょう。

　\(\displaystyle (2)=\frac{1}{2}\times (-2)+b\\ \\
2=-1+b\\ \\
3=b\)

これら求める直線 \(\ell\) は

　\(\displaystyle \underline{y=\frac{1}{2}x+3}\)

もちろん点Bを代入しても同じ式が出てきます。

連立方程式を利用する場合、
　求める直線を　\(y=ax+b\) 　とおいて、
　\(\displaystyle \mathrm{A}(\,-2\,,\,2\,)\hspace{8pt}\mathrm{B}\left(\,3\,,\,\frac{9}{2}\right)\)
を代入します。

　\( \begin{cases}
\hspace{7pt} 2=-2a+b\\ \\
\hspace{7pt} \displaystyle \frac{9}{2}=3a+b
\end{cases}\)

連立方程式の処理の基本は一文字消去です。

下の方程式を2倍して、
　\(9=6a+2b　･･･①\)
上の方程式を2倍して
　\(4=-4a+2b　･･･②\)
①-②より \(b\) を消去して
　\(5=10a\)　から　\(\displaystyle a=\frac{1}{2}\)
これを①か②かその前のどれかに代入して、\(b\) を求めます。
②に代入してみましょう。（どれでも同じです。）
　\(\displaystyle 4=-4\times \left(\frac{1}{2}\right)+2b\\ \\
4=-2+2b\\ \\
6=2b\\ \\
3=b\)

よって求める直線 \(\ell\) は
　\(\displaystyle \underline{y=\frac{1}{2}x+3}\)
と同じものが出てきます。

分数が混じっているので計算がややこしそうに見えますが、ほとんどの場合は傾きから求める方が楽ですよ。ここでもこの程度の計算は楽な方です。

比例定数の決定方法

(2)　\(a\) の値を，途中の説明も書いて求めなさい。その際，解答用紙の図を用いて説明しても良いものとします。

解答用紙の図は最初に問題についている図のことです。
解答用紙にも書いてくれているという、受験生の手間を省いてくれているものすごく親切な問題です。

「途中の説明も書いて」は答えを出すときの考えた順序で書けば良いのです。

そもそも \(a\) とは何か？
② \(y=ax^2\) の比例定数のことです。

だから②上の1点を見つければ良いだけです。
条件は、　\(\mathrm{AC}:\mathrm{CE}=1:3\)　しかありません。

直線が傾きを持っていてわかりにくいかもしれませんが、
　\(\mathrm{A,C,E}\)の \(x\) 座標の差（間隔）も 1：3 になります。

　\(\mathrm{A}\) の \(x\) 座標は\(-2\)，\(\mathrm{E}\) の \(x\) 座標は \(0\)
なので、この差「\(2\)」を4等分すればわかりやすくなります。
　\(\mathrm{A}\) と \(\mathrm{E}\) の中点の \(x\) 座標は \(-1\)
さらにその半分左に寄ると点 \(\mathrm{C}\) の \(x\) 座標なので,
　\(\mathrm{C}\) の \(x\) 座標は　\(\displaystyle -\frac{3}{2}\)

この \(\mathrm{C}\) は \(\ell\) 上の点なので \(y\) 座標もわかります。
　 \(\ell　:　\displaystyle y=\frac{1}{2}x+3\)

に \(\displaystyle x=-\frac{3}{2}\)　を代入して
　\(\begin{eqnarray}
\displaystyle y&=&\frac{1}{2}\times \left(-\frac{3}{2}\right)+3\\
\displaystyle &=&-\frac{3}{4}+3\\
\displaystyle &=&\frac{-3+12}{4}\\
\displaystyle &=&\frac{9}{4}
\end{eqnarray}\)

よって点\(\mathrm{C}\)の座標は
　\(\displaystyle \mathrm{C}\left(\,-\frac{3}{2}\,,\,\frac{9}{4}\,\right)\) 　

この点\(\mathrm{C}\)は②も通っています。
② \(y=ax^2\) は1点あれば比例定数が決まるので点\(\mathrm{C}\)を代入すると
　\(\begin{eqnarray}
\displaystyle \frac{9}{4}&=&a\left(-\frac{3}{2}\right)^2\\
\displaystyle \frac{9}{4}&=&\frac{9}{4}a\\
1&=&a
\end{eqnarray}\)

　∴　\(\underline{a=1}\)

関数の攻略法

関数で難しく感じるのは、途中が抜けているからです。
(1)を見てわかるように交点がわかれば直線が求まります。
(2)を見てわかるように点が与えられていれば比例定数は簡単に求まります。

つまり、
　\(\color{blue}{\fbox{交点がすべてわかればすべての直線や曲線}}\)
　\(\color{magenta}{\fbox{直線や関数がわかれば交点もすべて}}\)
求まります。

しかし、誘導にはすべては入っていません。
その抜けている部分を自分でやるかやらないか、それでほとんどが決まります。

中には座標を文字設定する応用問題もありますが、満点を狙わない人は捨てて良いです。笑

ただ、試験時間は限られています。
中学生の場合、ここ、関数にどれだけ時間を書けるかは大きな差となります。

(3)　右の図2のように，直線OC，OD をひき，

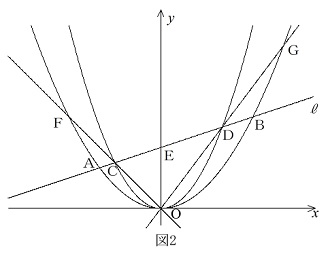
曲線①との交点をF,G とします。四角形CDGF
の面積を求めなさい。
　ただし、座標軸の単位の長さを 1 cm とします。

実際にの試験問題にあるグラフはもっと大きいので試験で使えます。
ここで自分で書き込むことをやろうという人は、正確で無くても良いので大きめのグラフを書いて考えてみて下さい。

考えることがあまりないということがわかります。

(1)(2)と続いて(3)がある場合、(1)(2)で出てきた答えは使うことがほとんどですよ。
今まで誘導されたことを無視しないで下さいね。

わかっていることを書き出しておきましょう。

　\(\ell　：　\displaystyle y=\frac{1}{2}x+3\)
　\(\mathrm{A}\,(-2\,,\,2\,)\)　\(\displaystyle \mathrm{B}\,\left(3\,,\,\frac{9}{2}\,\right)\)
　\(\displaystyle \mathrm{C}\,\left(-\frac{3}{2}\,,\,\frac{9}{4}\,\right)\)　\(\mathrm{D}\,(2\,,\,4\,)\)

ここからです。

　直線 OC の延長と曲線①との交点が F
　直線 OD の延長と曲線①との交点が G

F、G の座標も出しておきたいので直線 OC、OD も求めます。

これらは原点を通るので比例だから　\(y=ax\)　の形です。

直線 OC は　\(\displaystyle \mathrm{C}\,\left(-\frac{3}{2}\,,\,\frac{9}{4}\,\right)\)　を通るので、
　\(\displaystyle \frac{9}{4}=a\times \left(-\frac{3}{2}\right)\)
これから
　\(\displaystyle a=-\frac{9}{4}\times \frac{2}{3}=-\frac{3}{2}\)

よって直線 OC は　 \(\displaystyle y=-\frac{3}{2}x\)

原点を通る比例だから切片は最初から考えなくて良いですね。

同じように直線ODの式も出します。

別に暇だからやっているのではありません。必要だからやっているのです。

直線 OD は　\(\mathrm{D}\,(2\,,\,4\,)\)　を通る原点を通る直線（\(y=ax\)）なので、
　\(4=a\times 2\)　から　\(a=2\)

よって直線 OD は　\(y=2x\)

さて、点F、G の座標を出しましょう。
面積を求めるのですべての点の座標は出さなくてはなりません。

この段階の誘導が飛んでいるのです。
意地悪くしているのではなく、ここで差がつくようにしているのです。
それに、これすべてを小問にしていたら筋道を立てるという部分を試験できません。

点Fは、①と直線 OC との交点です。

交点といえば連立、は常識ですよね。

　\( \begin{cases}
\hspace{7pt}\displaystyle y=\frac{1}{2}x^2\\
\hspace{7pt}\displaystyle y=-\frac{3}{2}x
\end{cases}\)

より
　\(\begin{eqnarray}
\displaystyle \frac{1}{2}x^2&=&-\frac{3}{2}x\\
x^2&=&-3x\\
x^2+3x&=&0\\
x(x+3)&=&0\\
x&=&0,-3
\end{eqnarray}\)

\(x=0\)　は原点のことなので交点 F の \(x\) 座標は \(-3\)

直線OC　\(\displaystyle y=-\frac{3}{2}x\) に \(x=-3\) を代入すると、
　\(\displaystyle y=-\frac{3}{2}\times (-3)=\frac{9}{2}\)

よって　\(\displaystyle \mathrm{F}\,\left(\,-3\,,\,\frac{9}{2}\right)\)

同じように点 F は、①と直線 OC との交点です。

　\( \begin{cases}
\hspace{7pt}\displaystyle y=\frac{1}{2}x^2\\
\hspace{7pt} y=2x
\end{cases}\)

より
　\(\begin{eqnarray}
\displaystyle \frac{1}{2}x^2&=&2x\\
x^2&=&4x\\
x^2-4x&=&0\\
x(x-4)&=&0\\
x&=&0,4
\end{eqnarray}\)

\(x=0\)　は原点のことなので交点 G の \(x\) 座標は \(4\)

\(y\) 座標は \(y=2x\) に　\(x=4\)　を代入して
　\(y=2\times (4)=8\)

よって　\(\mathrm{G}\,(\,4\,,\,8)\)

ここまでをグラフに書き込んでみます。
実際には、1つ出たら書き込む、ということを続けていけば良いですよ。
まとめて書き込むより確実です。
ここでは図を少なくしたいのでまとめて書くだけです。笑

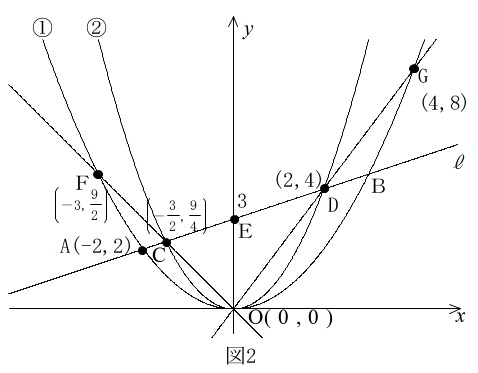
四角形CDGFの面積を求めるので、本当はこれで十分答えは出せます。
ちょっとした公式を覚えておけば数十秒もあれば答えが出ます。
（もしも、私の生徒がこれを見ていたら、すぐに答えだして良いですよ。）

しかし、普通の中学生がこの四角形の面積を求めるには四角形の形を特定する必要があります。
しかもそれは答えにたどり着ける情報かどうかもわかりません。

後で確認してみましょう。

四角形の面積は三角形の2つ分

例えば、四角形が台形だったとしても、軸に平行な直線でない場合は、2点間の距離で線分（上底と下底）の長さを出すのに苦労することがあります。

そこで、ほとんどに通用する三角形の面積を利用することを考えます。

四角形の面積を求めるということは、三角形の面積が元になっているという事実を使えば、どのような四角形でも「三角形の和」と考えることができるので関数の場合に限らなくても、三角形の面積で考えてみる、ということを優先すると良いです。

だから、ここでは三角形の面積を求める形で説明します。

分かり易いようにちょっと図に書き足します。

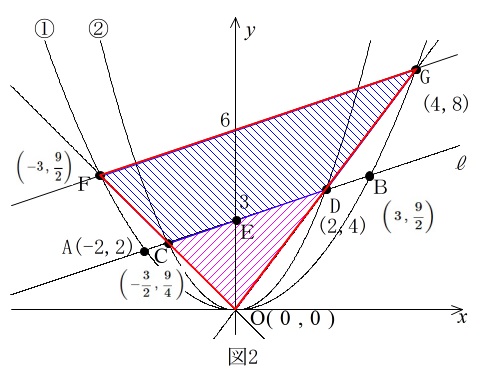
後先逆になりましたが、直線 FG は、
　\(\displaystyle \left(\hspace{6pt}-3\hspace{10pt},\hspace{10pt}\frac{9}{2}\hspace{10pt}\right)\)
　\((\hspace{15pt}4\hspace{12pt},\hspace{12pt}8\hspace{12pt})\)

この2点を通るので直線 FG を1次関数 \(y=ax+b\) とすると

　\(\begin{eqnarray}
\displaystyle a&=&\frac{8-(\frac{9}{2})}{4-(-3)}= \frac{\frac{7}{2}}{7}= \frac{7}{2}\times \frac{1}{7}\\
\displaystyle &=& \frac{1}{2}
\end{eqnarray}\)

これから　\(\displaystyle y=\frac{1}{2}x+b\)

これに点 F,G どちらかを代入すると \(b\) が求まります。
　\(\mathrm{G}\,(\,4\,,\,8\,)\)
を代入すると
　\(\displaystyle 8=\frac{1}{2}\times (4)+b\\ \\
8=2+b\)
これから　\(b=6\)

よって直線FGは
　\(\displaystyle y=\frac{1}{2}x+6\)

（この式を求めるところは別紙で簡単に求めておけば良いですよ。）

傾きが同じなのでこれは \(\ell\) と平行だということがわかります。
四角形CDGFは台形だということはわかりますが、上底と下底を2点間の距離で出したとして、高さはどうしますか？

垂線下ろして、、、なんてことはしません。
高校生なら点と直線の距離の公式を使って、ということもできますがしません。

図を見て気がついていると思いますが、

大きい三角形 OFG から小さい三角形 OCD を引きます。

　\(四角形\mathrm{CDGF}＝\color{red}{\triangle \mathrm{OFG}} -\color{magenta}{\triangle \mathrm{OCD}}\)

この面積計算はいろいろ考えられますが、一番多い形で求めてみましょう。
（何度も言いますが私の生徒はもっと簡単に答えを出してかまいません。）
　\(\triangle \mathrm{OFG}\)　の面積は
直線 FG の切片と原点を結ぶ線分を底辺として三角形を2つに分けます。

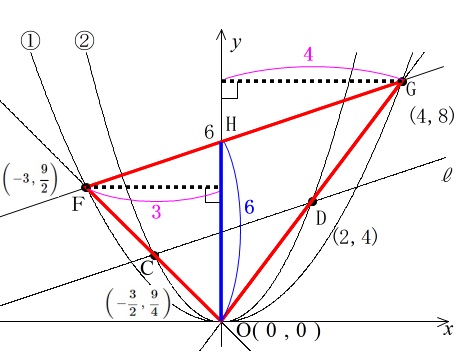
直線 FG の切片を H とすると、底辺 OH とする三角形に2つに分けることができます。

　\(\color{red}{\triangle \mathrm{OFG}=\triangle \mathrm{OFH}+\triangle \mathrm{OGH}}\)

2つの三角形の底辺は共通で　\(\mathrm{OH}=6\)　となっています。

高さは、
　\(\color{red}{頂点から y 軸への垂線の長さ}\)
になりますのでそれぞれの \(x\) 座標です。

よって

　\(\begin{eqnarray}
\triangle \mathrm{\color{red}{OFG}}&=&\triangle \mathrm{OFH}+\triangle \mathrm{OGH}\\
\displaystyle &=&\frac{1}{2}\times \color{blue}{6}\times \color{magenta}{3}+\frac{1}{2}\times \color{blue}{6} \times \color{magenta}{4}\\ &=&9+12\\
&=&\color{red}{21}
\end{eqnarray}\)

これから　\(\color{magenta}{\triangle \mathrm{OCD}}\)　の面積を引けば良いのです。

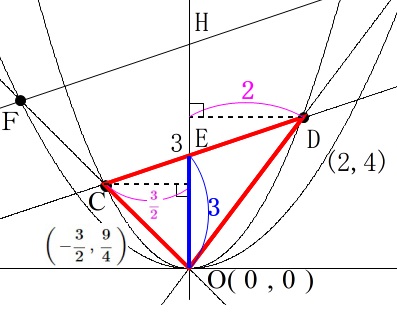
　\(\begin{eqnarray}
\color{magenta}{\triangle \mathrm{OCD}}&=&\triangle \mathrm{OCE}+\triangle \mathrm{ODE}\\
\displaystyle &=&\frac{1}{2}\times \color{blue}{3}\times \color{magenta}{\frac{3}{2}}+\frac{1}{2}\times \color{blue}{3} \times \color{magenta}{2}\\
\displaystyle &=&\frac{9}{4}+3\\
\displaystyle &=&\frac{9+12}{4}\\
&=&\color{magenta}{\frac{21}{4}}
\end{eqnarray}\)　　
　
よって求める四角形 CDGF の面積は

　\(\begin{eqnarray}
四角形\mathrm{CDGF}&=&\color{red}{\triangle \mathrm{OFG}} -\color{magenta}{\triangle \mathrm{OCD}}\\
\displaystyle &=&\color{red}{21}-\color{magenta}{\frac{21}{4}}\\
\displaystyle &=&\frac{84-21}{4}\\
\displaystyle (答え)&=&\frac{63}{4}\hspace{10pt}(\mathrm{cm^2})
\end{eqnarray}\)

ここまできて何ですが、
分数計算のときは分母を一つにして、分子の計算に集中すると計算ミスは減ります。

さて答えの数値は出ましたが、一つ説明を加えておきます。

問題の単位の説明で、
　「座標軸の単位の長さを 1 cmとします。」
と書いてあります。

詳しくすると長くなりますので簡単に言うと、
　「座標軸の 0 から 1 まで」
を座標の単位といいますので、座標上での長さをそのまま cm として単位をつけて考えて良いですよ、ということです。