2019年(平成31年)度に埼玉県で行われた公立高校入試数学の第3問と第4問の解説です。
ともに学校選択問題の第3問第4問と同じ問題です。
関数は座標上の面積と面積比に関する座標の一般的な文字設定問題で、
平面図形は円と円周角の関係と面積の問題で対称性を利用します。
※（依頼人です。）
2019年(平成31年)度埼玉県公立高校入試終わりましたね。
受験生のみなさん、お父さんお母さんお疲れさまでした。
早速、受験個別指導のプロとして全国で活躍されているこの時期劇的にお忙しい柏田先生に無理を言ってお願いし2019年(平成31年)度の埼玉県公立高校入試の数学の解説をしていただきました。
今回の解説も前回（2018年 平成30年度）同様、永久保存版にしても良いくらい価値がありますよ。
では、第3.4問目の超強力な解説をご覧下さい。
アッ！
早く早くと無理を言って解説をお願いしていることもあり、柏田先生はちょっと不十分と感じているようで、追記していくのでよろしくお願いしますとのことです。
私としてはそんなことないのになぁ～ と思うのですが・・・
なので、追記も楽しみにしていてください！
問題は埼玉県の公式ページでも公開してくれています。
第3問関数問題
\(\large{3}\) \(\color{red}{\fbox{ 学校選択問題の3 }}\)
(1)に入る前の条件はすべてに通じる条件です。
\(\color{red}{\fbox{ 条件 }}\)
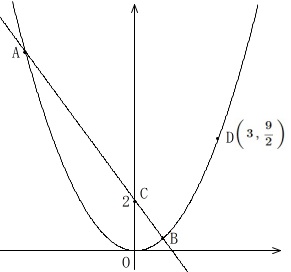
曲線は\(\displaystyle \,y=\frac{1}{2}x^2\,\)
直線は\(\,y=ax+2\,(\,a\,＜\,0\,)\,\)
交点\(\,\mathrm{A}\,\)は\(\,x\,\)座標が負、\(\,\mathrm{B}\,\)は\(\,x\,\)座標が正
直線の\(\,y\,\)切片を\(\,\mathrm{C}\,\)
点\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,3\,\)
これから分かることを出しておきましょう。
交点と直線はできるだけ求めて座標上に示しておくと良いです。
\(\,\mathrm{C}\,\)の座標は\(\,(\,0\,,\,2\,)\,\)
\(\,\mathrm{D}\,\)は\(\,x=3\,\)の放物線上の点なので
\(\displaystyle \,y=\frac{1}{2}\times (3)^2=\frac{9}{2}\,\)
から
\(\displaystyle \,\mathrm{D\,\left(\,3\,,\,\frac{9}{2}\,\right)}\,\)
(1)
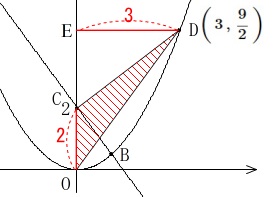
\(\,△\mathrm{OCD}\,\)の面積です。
\(\,3\,\)点\(\,\mathrm{O,C,D}\,\)は固定された点なので底辺と高さを決めれば答えはすぐに出ます。
\(\,\mathrm{OC}\,\)を底辺と見ると\(\,y=ax+2\,\)の切片\(\,2\,\)が底辺で、
高さは\(\,\mathrm{D}\,\)の\(\,x\,\)座標\(\,3\,\)となるので
\(\begin{eqnarray}\displaystyle
\mathrm{△OCD}&=&\frac{1}{2}\times \mathrm{OC}\times \mathrm{DE}\\
&=&\frac{1}{2}\times 2\times 3\\
&=&\underline{ 3 }
\end{eqnarray}\)
(2)\(\,\mathrm{△ADC=4△CDB}\,\)になるときの\(\,a\,\)の値です。
\(\,a\,\)は直線の傾きなので、
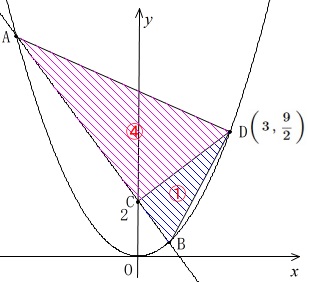
\(\,a\,\)が変わると\(\,\mathrm{A,B}\,\)も変わり面積比も変わります。
変わらないのは\(\,\mathrm{C,D}\,\)だけです。
\(\,\mathrm{△ADC=4△CDB}\,\)となるのは、
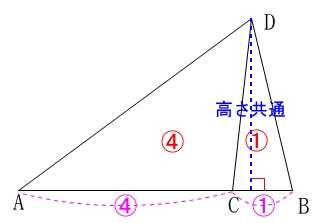
\(\,\mathrm{AC=4CB}\,\)
となるときなので、
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を\(\,\color{red}{t}\,\)とおくと、
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,\color{red}{-4t}\,\)となります。
\(\,\mathrm{B}\,\)の\(\,x\,\)座標は正なので\(\,t\,＞\,0\,\)です。
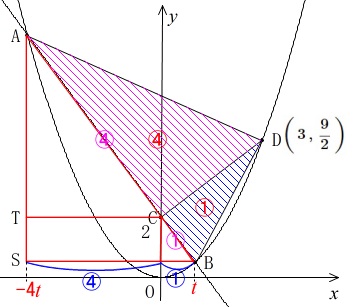\(\,\mathrm{A,B}\,\)は放物線上の点なので
\(\displaystyle \,\mathrm{B\,\left(\hspace{6pt}t\hspace{6pt},\,\frac{1}{2}t^2\,\right)}\,\)
\(\,\mathrm{A\,\left(\,-4t\,,\,8t^2\hspace{4pt}\right)}\,\)
\(\,2\,\)点間の距離でも良いのですが、
このとき\(\,\mathrm{AT:TS=\color{red}{4}:\color{red}{1}}\,\)でもあるので
\(\begin{eqnarray}
\mathrm{AT}&=&(8t^2)-(2)\\
&=&8t^2-2
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle
\mathrm{TS}&=&(2)-\left(\frac{1}{2}t^2\right)\\
&=&\frac{4-t^2}{2}
\end{eqnarray}\)
から
\(\begin{eqnarray}\displaystyle
(8t^2-2):\frac{4-t^2}{2}&=&\color{red}{4}:\color{red}{1}\\
8t^2-2&=&4\times \frac{4-t^2}{2}\\
8t^2-2&=&8-2t^2\\
8t^2+2t^2&=&8+2\\
10t^2&=&10\\
t^2&=&1\\
t&=&\pm 1
\end{eqnarray}\)
\(\,t＞0\,\)なので\(\,t=1\,\)
このとき\(\displaystyle \,\mathrm{B\,\left(\,1\,,\,\frac{1}{2}\right)}\,\)
これが\(\,y=ax+2\,\)を通るので
\(\begin{eqnarray}\displaystyle
\frac{1}{2}&=&a\times (1)+2\\
&=&a+2\\
a+2&=&\frac{1}{2}\\
a&=&\frac{1}{2}-2\\
&=&\underline{ -\frac{3}{2} }
\end{eqnarray}\)
もちろん\(\,t=1\,\)のとき\(\,\mathrm{A\,(\,-4\,,\,8\,)}\,\)を代入しても
\(\begin{eqnarray}\displaystyle
8&=&a\times (-4)+2\\
&=&-4a+2\\
4a&=&2-8\\
&=&-6\\
a&=&\frac{-6}{4}\\
&=&\underline{ -\frac{3}{2} }
\end{eqnarray}\)
と同じ値が出てきます。
この問題は、
「例えば\(\,\mathrm{B}\,\)の\(\,x\,\)座標が\(\,x=1\,\)だとすると面積比は？」
と試すことによって答えは偶然にも出てきます。笑
出題者の意図はそこではないとは思いますけど。
試験中に試して見る、という高等テクニック？を使える余裕のある人ほど答えが近かった問題でした。
第4問平面図形問題
\(\,\large{4}\,\) \(\color{red}{\fbox{ 学校選択問題の4 }}\)
図形問題で条件がありますので書き出します。
関数と同じで(1)の前にある条件はすべてに使える条件です。
\(\color{red}{\fbox{ 条件 }}\)
\(\,\mathrm{AB}\,\)は直径
\(\,\mathrm{AM:MP=2:1}\,\)
\(\,\mathrm{AB=6}\,\)
\(\,\mathrm{∠ABP=60^{\circ}}\,\)
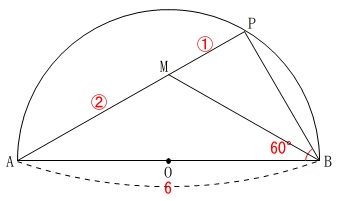これらの条件はすべて使わないと解けない条件です。
問題に与えられる条件で不要なものはありません。
\(\,\mathrm{AB}\,\)は直径
\(\,\mathrm{∠ABP=60^{\circ}}\,\)
から円周角が\(\,90°\,\)になるので\(\,\mathrm{△ABP}\,\)は三角定規だと分かります。
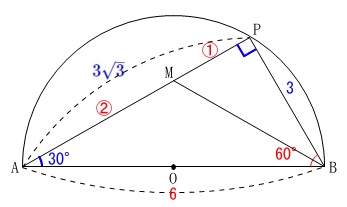三角定規の比から
\(\,\mathrm{PB:AB:AP=1:2:\sqrt{3}}\,\)
なので
\(\,\mathrm{AP=\color{blue}{3\sqrt{3}}}\,\)
条件から\(\,\mathrm{AM:MP=2:1}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{PM}&=&\mathrm{AP}\times \frac{1}{3}\\
&=&3\sqrt{3}\times \frac{1}{3}\\
&=&\underline{ \sqrt{3} }
\end{eqnarray}\)
この\(\,\mathrm{PM=\sqrt{3}}\,\)は(2)でも使える条件です。
分かったことは図に書き足しておきましょう。
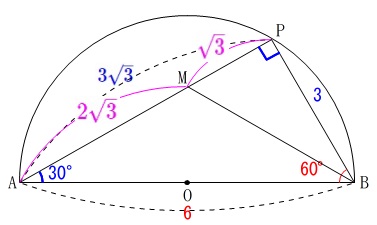\(\,\mathrm{△BPM}\,\)は直角三角形で
\(\,\mathrm{PM:BP=\sqrt{3}:3=1:\sqrt{3}}\,\)
となっているので\(\,\mathrm{△BPM}\,\)も三角定規の1つです。
このことから
\(\,\mathrm{\color{red}{∠MBP=∠MBO=30°}}\,\)
が言えます。
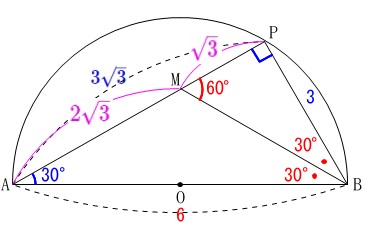
\(\,\mathrm{BP:BA=3:6=1:2}\,\)
\(\,\mathrm{PM:AM=1:2}\,\)
なので
角の二等分線定理
から
\(\,\mathrm{\color{red}{∠MBP=∠MBO=30°}}\,\)
は言えるのですが定理を忘れていた場合でも出せるということで示しておきました。
\(\,\mathrm{△MAB}\,\)が二等辺三角形
\(\,\mathrm{△BMP}\,\) ≡ \(\,\mathrm{△BMO}\,\)
ということなどもわかります。
本来の作業としては分かることはすべて書いておく方が良いですが、必要ないかもしれないので先に進みます。
余裕がある場合は分かることはすべて書き込んでおくと後の問題は終わっていることが多いです。
ただ、試験会場での受験生にはあまり余裕がないと思われるので、先に進んで問題に合わせて条件を書き込むことにします。
(2)
条件が加わります。
\(\,\mathrm{BM}\,\)の延長と\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{AP}} }\,\)との交点を\(\,\mathrm{Q}\,\)
\(\,\mathrm{OP}\,\)と\(\,\mathrm{BQ}\,\)との交点を\(\,\mathrm{R}\,\)
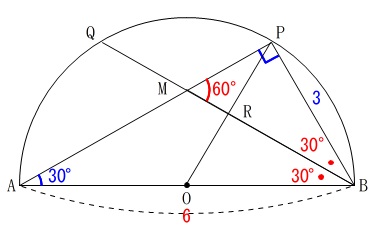とします。
①
問題は\(\,\mathrm{BQ}\,\)を折り目として半円\(\,\mathrm{O}\,\)を折ると、
点\(\,\mathrm{P}\,\)と点\(\,\mathrm{O}\,\)が重なることを説明することです。
つまり、対称移動していることを示すことになります。
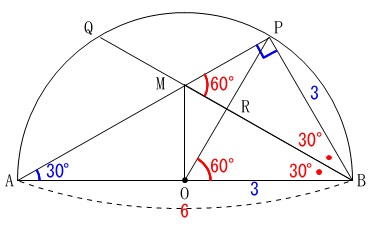
\(\,\mathrm{△BOP}\,\)は正三角形です。
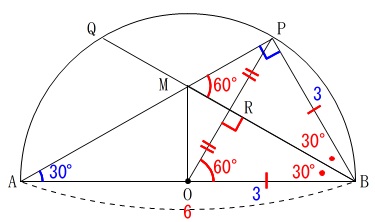
\(\,\mathrm{∠B}\,\)の二等分線\(\,\mathrm{BQ}\,\)は底辺\(\,\mathrm{OP}\,\)を垂直に二等分する
ので
対称の軸\(\,\mathrm{BQ}\,\)で折ると\(\,\mathrm{P}\,\)と\(\,\mathrm{O}\,\)は重なります。
二等辺三角形の定理ですが、正三角形も二等辺三角形の1つです。
他にも\(\,\mathrm{△BOR}\,\) ≡ \(\,\mathrm{△BPR}\,\)をいっても対称性から重なることは言えます。
何をどう使おうが問題の事実は成り立つので説明しろと言われる方が難しいですね。笑
ただ、折り返して重なるということは、
\(\,2\,\)点が対称（線対称）移動した点どうしになっている
ことを示すことになるので、注意しておきましょう。
②
公式の使えない面積を求めます。
公式が使えない面積を求めるときは、
『部分』＋『部分』
『全体』－『部分』
を計算することになります。
比を利用する場合もありますが、『全体』－『部分』を省略しているだけです。
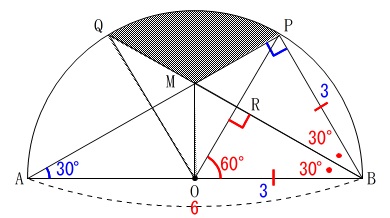かげの部分の面積を求めます。
扇形の選び方で計算方法は変わりますがどれもたいして変わらないでしょう。
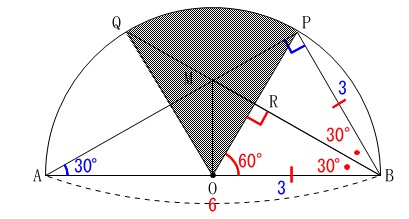この影から
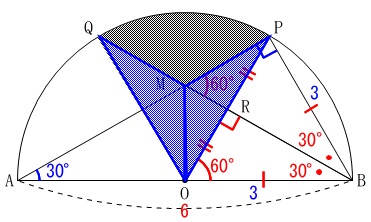青い部分の三角形2つ分を引きます。
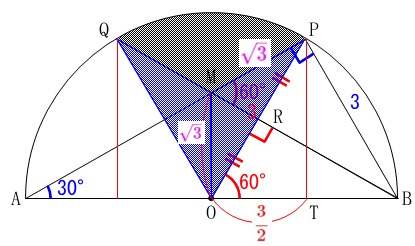
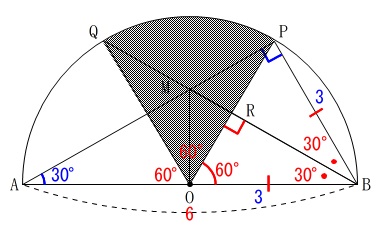影の扇形の中心角は\(\,60°\,\)なので、
\(\begin{eqnarray}
(扇形の面積)&=&\pi\times (3)^2\times \frac{60}{360}\\
&=&\frac{3}{2}\pi
\end{eqnarray}\)
青い影の2つの三角形は合同なので\(\,\mathrm{△OMP}\,\)を2倍します。
\(\,\mathrm{△OMP}\,\)は\(\,\mathrm{OM}\,\)を底辺、高さを\(\,\mathrm{OT}\,\)とする三角形なので
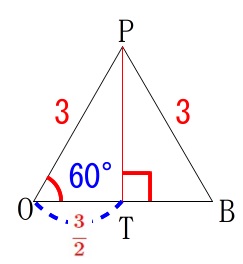
\(\begin{eqnarray}\displaystyle
\mathrm{△OMP}&=&\frac{1}{2}\times \sqrt{3}\times \frac{3}{2}\\
&=&\frac{3\sqrt{3}}{4}
\end{eqnarray}\)
よって求める影の部分の面積は扇形の面積から\(\,\mathrm{△OMP}\,\)を2つ分引いて、
\(\displaystyle \hspace{10pt}\frac{3}{2}\pi-\frac{3\sqrt{3}}{4}\times 2\\
\displaystyle =\frac{3}{2}\pi-\frac{3\sqrt{3}}{2}\\
\displaystyle =\underline{ \frac{3\pi-\sqrt{3}}{2} }\)
他にも解法はいろいろ考えられます。
数学の答えは1つでも解法は1つではありません。
ただ、試験時間を考えると迷っているヒマはないのである程度図に書き込みが終われば、
思いついた解法で突っ走った方がはやいですよ。
計算自体は大して時間かかりません。
以上です。
⇒ 埼玉県公立高校入試(平成30年度)の数学過去問題の解説と対策
2018年度と合わせて何が大切かを理解しておくと良いです。
⇒ 2019年(平成31年)度埼玉県公立高校入試数学の問題と解説
1は配点が半分以上ある小問集合です。
学校選択問題と重複する問題もあるのでさらっと行くものばかりではないですね。
⇒ 2019年(平成31年)度埼玉県公立高校入試数学第2問の解説
2も小問題集合ですが作図は見慣れない角度だったかもしれません。
学校選択問題の解説ページです。